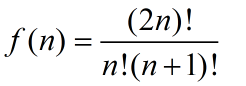考研数据结构笔记

发表于 2024/07/29 更新于 2024/08/30

作者 MasterKe

24 分钟阅读

栈

括号匹配

        
      
#include <stdio.h>
#include <stdlib.h>
#include <stdbool.h>

#define MAXSIZE 10

typedef struct
{
    char data[MAXSIZE];
    int top;
} SqStack;

// 初始化顺序栈
void initStack(SqStack *S)
{
    S->top = -1;
}

// 判断是否为空
bool isEmpty(SqStack *S)
{
    return S->top == -1;
}

// 判断是否满
bool isFull(SqStack *S)
{
    return S->top == MAXSIZE - 1;
}

// 入栈
bool Push(SqStack *S, char *x)
{
    if (isFull(S))
        return false;
    S->data[++S->top] = *x;
    return true;
}

// 出栈
bool Pop(SqStack *S, char *x)
{
    if (isEmpty(S))
        return false;
    *x = S->data[S->top--];
    return true;
}

//检查字符串是否合法
bool checkString(char str[])
{
    int length = 0;
    int i = 0;
    while (str[i++] != '\0')
    {
        length++;
    }
    SqStack S;
    initStack(&S);
    for (int i = 0; i < length; i++)
    {
        if (str[i] == '(' || str[i] == '{' || str[i] == '[' || str[i] == ')' || str[i] == '}' || str[i] == ']')
        {

            if (str[i] == '(' || str[i] == '{' || str[i] == '[')
                Push(&S, &str[i]);
            else
            {
                if (isEmpty(&S))
                    return false; // 匹配到右括号且栈空，不合法

                char topElem;
                Pop(&S, &topElem);
                if (str[i] == ')' && topElem != '(')
                    return false;
                if (str[i] == '}' && topElem != '{')
                    return false;
                if (str[i] == ']' && topElem != '[')
                    return false;
            }
        }
    }
    return isEmpty(&S);
}

char a[10] = "(你好){}";
void main()
{
    if (checkString(a))
    {
        printf("括号合法");
    }
    else
    {
        printf("括号不合法");
    }
}

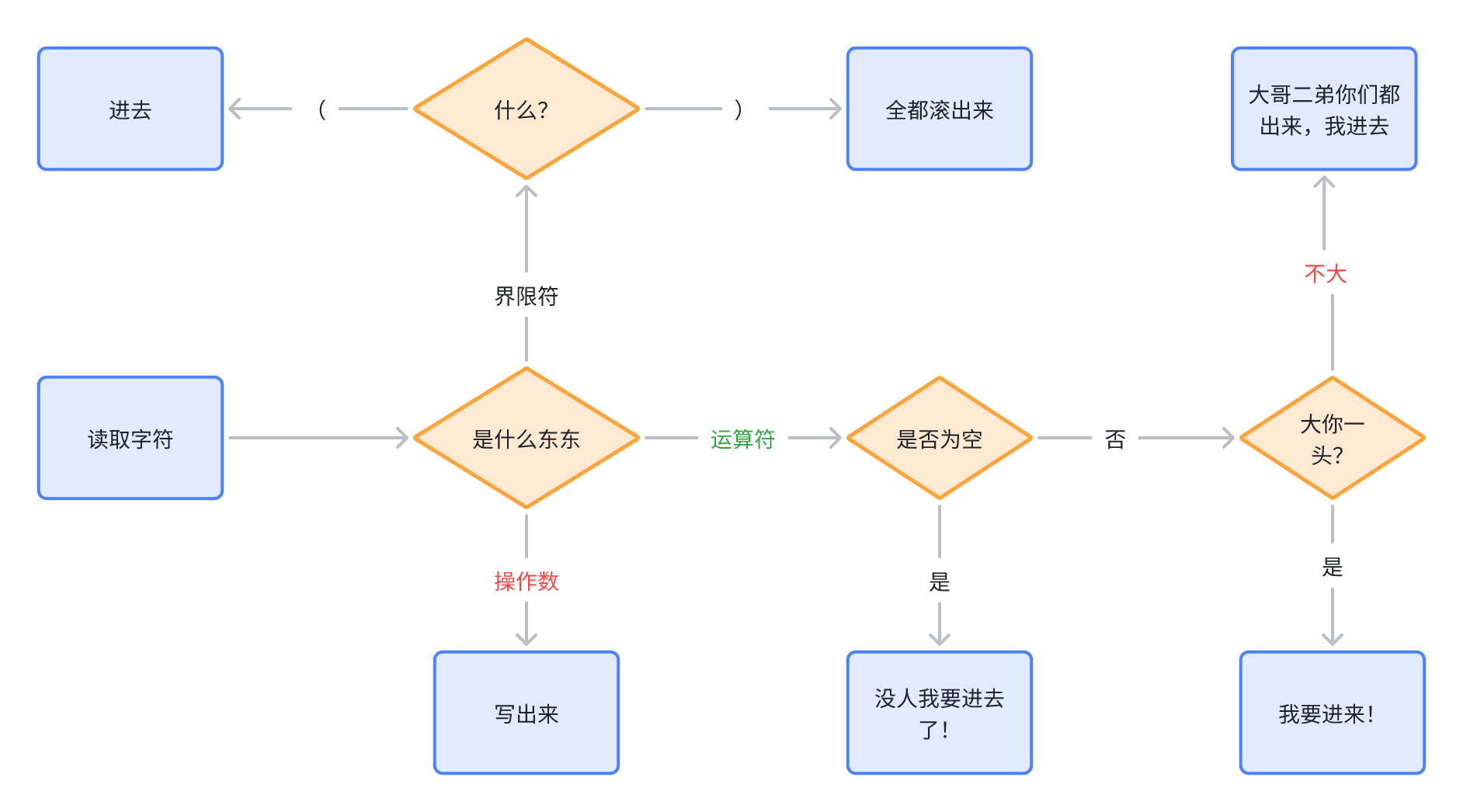
中缀转后缀机算

数组和特殊矩阵

核心思想：总=满+零

例如：i行j列元素有i-1行满和j个零。

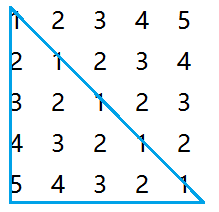
对称矩阵

        
      
=================================
若以行优先进行：
对于矩阵a[i][j]压缩=>B[k],若i,j都从0开始

第1行 1个元素
第2行 2个元素
···
第i-1行 i-1个元素
第i行 i个元素

a[i][j]存储在B中第多少个位置分析如下:
第i行前有i-1行满的,满元素的行就有:
[1+(i-1)]*(i-1)/2=i(i-1)/2
再看元素所在行第几个
第j个从左往右数,所以是在第j个元素

总=i(i-1)/2+j [若下标从0开始,-1即可]
=================================
=================================
若以列优先进行：
对于矩阵a[i][j]压缩=>B[k],若i,j都从0开始

第1行 n个元素
第2行 n-1个元素
···
第j-1行 n-(j-1)+1=n-j+2个元素
第j行 n-j+1个元素 [每行减j个,少1个加回去]

a[i][j]存储在B中第多少个位置分析如下：
第j列前有j-1列满的,满元素的行就有:
[n+(n-j+2)](j-1)/2
再看元素所在列第几个
第i个从上往下数
第1列说5其实就是5,实际存了5个元素
第2列说5其实是4,实际存了4个元素
所以第i行说i其实是在第i-j+1个元素,实际存了i-j+1个元素
另外,j=i的时候是对角线上的元素,i-j为0,但对角线上的元素一定是第一个元素,所以+1,为什么是i-j而不是j-i呢？因为这里下半角矩阵i是≥j的

三角矩阵

三对角矩阵

树和二叉树

树的性质

树的节点数n等于所有结点的度总和+1。
度为m的树第i层最多有m的i-1次方个结点（i≥1）。
高度为h的m叉树最多节点树为：

\[\frac{m^h-1}{m-1}\]

第一行有m^0个
第二行有m^1个
第三行有m^2个
第四行有m^3个
第h行有m^h-1个
利用等比数列求和公式即可解出

度为m有n个结点的树最小高度是： ${\lceil}log_m(n(m-1)+1){\rceil}$

加一向下取整就是直接向上取整。

具有n个结点、度为m的树最大高度是n-m+1。
高度为h、度为m的树最少有n+m-1个结点。

二叉树

非空二叉树叶子结点🍃的个数度为2的结点的个数+1。
完全二叉树的最后一个分支结点是${\lfloor}\frac{n}{2}{\rfloor}$
第i层最多有$2^{i-1}$个结点。
n个结点最多有n+1个空指针。
满二叉树的结点数为：$2^h-1$
n个节点最多有多少种形态

线索二叉树

x结点的前驱后继：

	中序线索二叉树	先序线索二叉树	后序线索二叉树
前驱	左子树的最右下结点	✖	有右子树=>前驱是右子节点无右子树=>前驱是左子节点
后继	右子树的最左下结点	有左子树，则后继是左子节点没有左子树但有右子树，则是右子节点如果左右子树都没有，则该节点是单节点或叶子节点。	✖

        
      
#include <stdio.h>
#include <stdlib.h>

typedef struct threadBitNode
{
    char value;
    struct threadBitNode *lchild;
    struct threadBitNode *rchild;
    int ltag;
    int rtag;
} threadBitNode, *threadBitTree; // 分别定义二叉结点和二叉树
threadBitNode *pre = NULL;
void visit(threadBitNode *T)
{
    // printf("值为：%c\n", T->value);
    if (T->lchild == NULL)
    {
        T->lchild = pre;
        T->ltag = 1;
        if (pre != NULL)
            printf("左线索化：%c=>%c\n", T->value, pre->value);
        else
            printf("左线索化：%c=>%c\n", T->value, pre);
    }
    if (pre != NULL && pre->rchild == NULL)
    {
        pre->rchild = T;
        pre->rtag = 1;
        printf("右线索化：%c=>%c\n", pre->value, T->value);
    }
    pre = T;
}
void inThread(threadBitTree T)
{
    if (T != NULL)
    {
        inThread(T->lchild); // 遍历左子树
        visit(T);
        inThread(T->rchild); // 遍历右子树
    }
}

threadBitNode *createNewNode(char v)
{
    threadBitNode *newNode = (threadBitNode *)(malloc(sizeof(threadBitNode)));
    newNode->value = v;
    newNode->lchild = NULL;
    newNode->rchild = NULL;
    return newNode;
}

int main()
{
    // 初始化二叉树
    threadBitTree root = createNewNode('A');
    root->lchild = createNewNode('B');
    root->rchild = createNewNode('C');
    root->lchild->lchild = createNewNode('D');
    root->lchild->rchild = createNewNode('E');
    root->lchild->lchild->rchild = createNewNode('G');
    root->rchild->lchild = createNewNode('F');
    inThread(root);
    pre->rchild = NULL;
    pre->rtag = 1;
    printf("右线索化：%c=>%c\n", pre->value, NULL);
    return 0;
}

图

无向图

无向图的边的取值范围是$0{\sim}\frac{n(n-1)}{2}$，因为每一条边都可以最多连接n-1，两两抵消除以2，最多边的情况下的无向图被称为完全图
无向图中的极大连通子图被称为连通分量（可以类比极大线性无关组）
所有顶点都连通的无向图被称为连通图，连通图最少有n-1条边，非连通图最多有$C^2_{n-1}$条边

有向图

有向图中的极大强连通子图被称为强连通分量
所有顶点都连通的有向图被称为强连通图，强连通图最少有n条边（形成回路）

简单图

拓扑排序：https://oi-wiki.org/graph/topo/

子图

并非所有的子集都可以构成子图，如果只有边而没有带上顶点那么就根本不满足图的概念
所有的顶点和边都属于图G的图称为G的子图。含有G的所有顶点的子图称为G的生成子图。

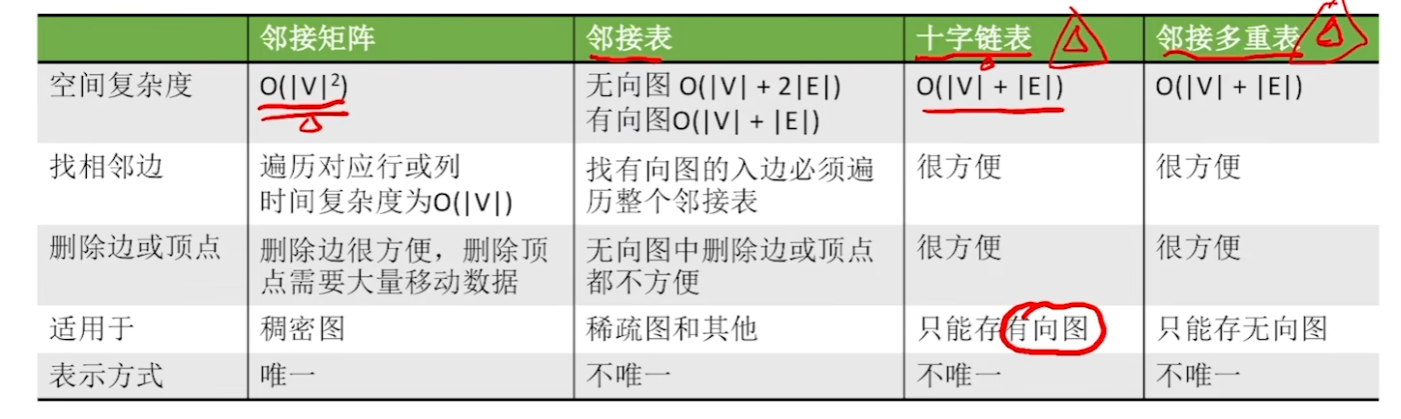
邻接矩阵法

领接表

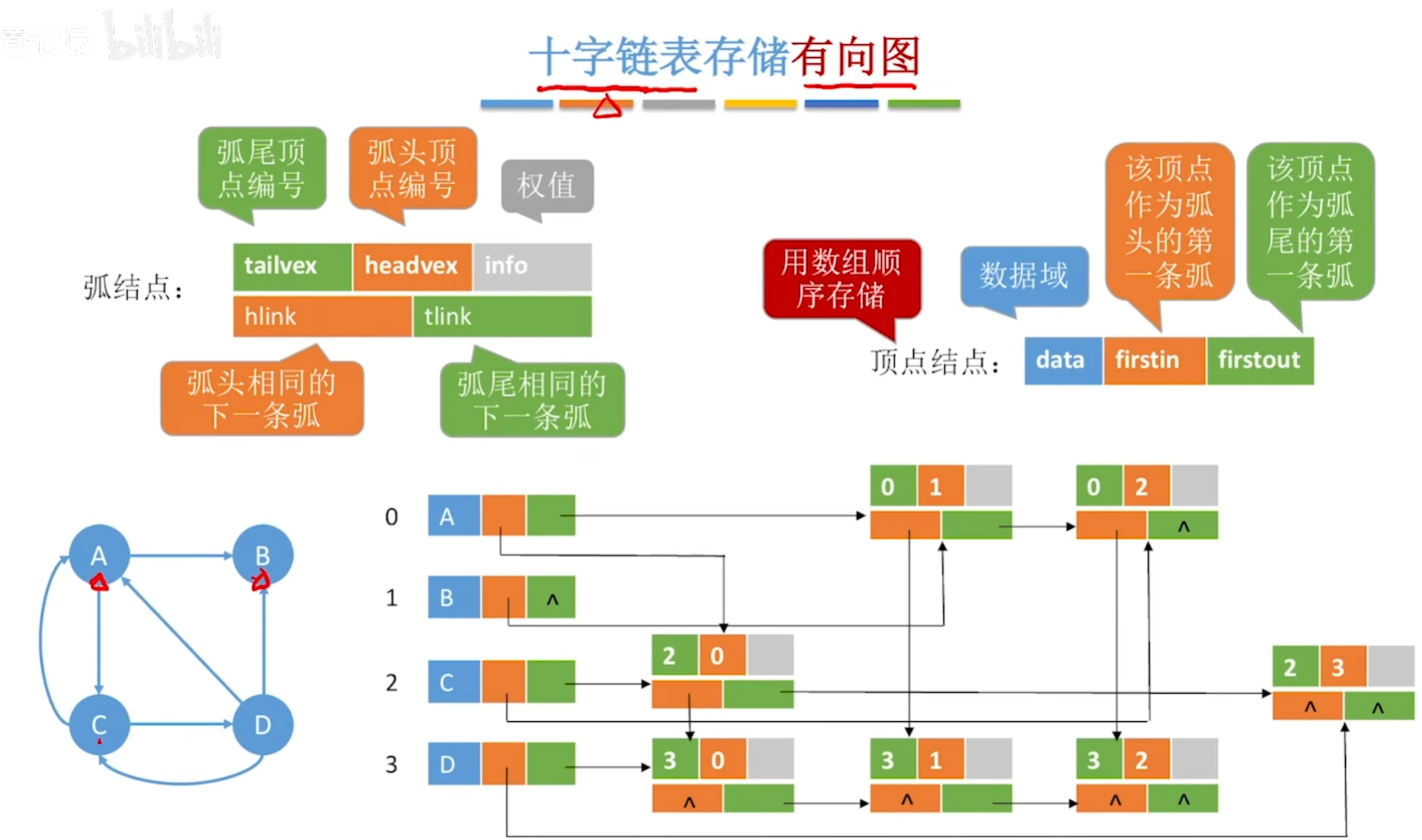
十字链表

绿色指针本来就是要连接的，加一个橙色找入度。

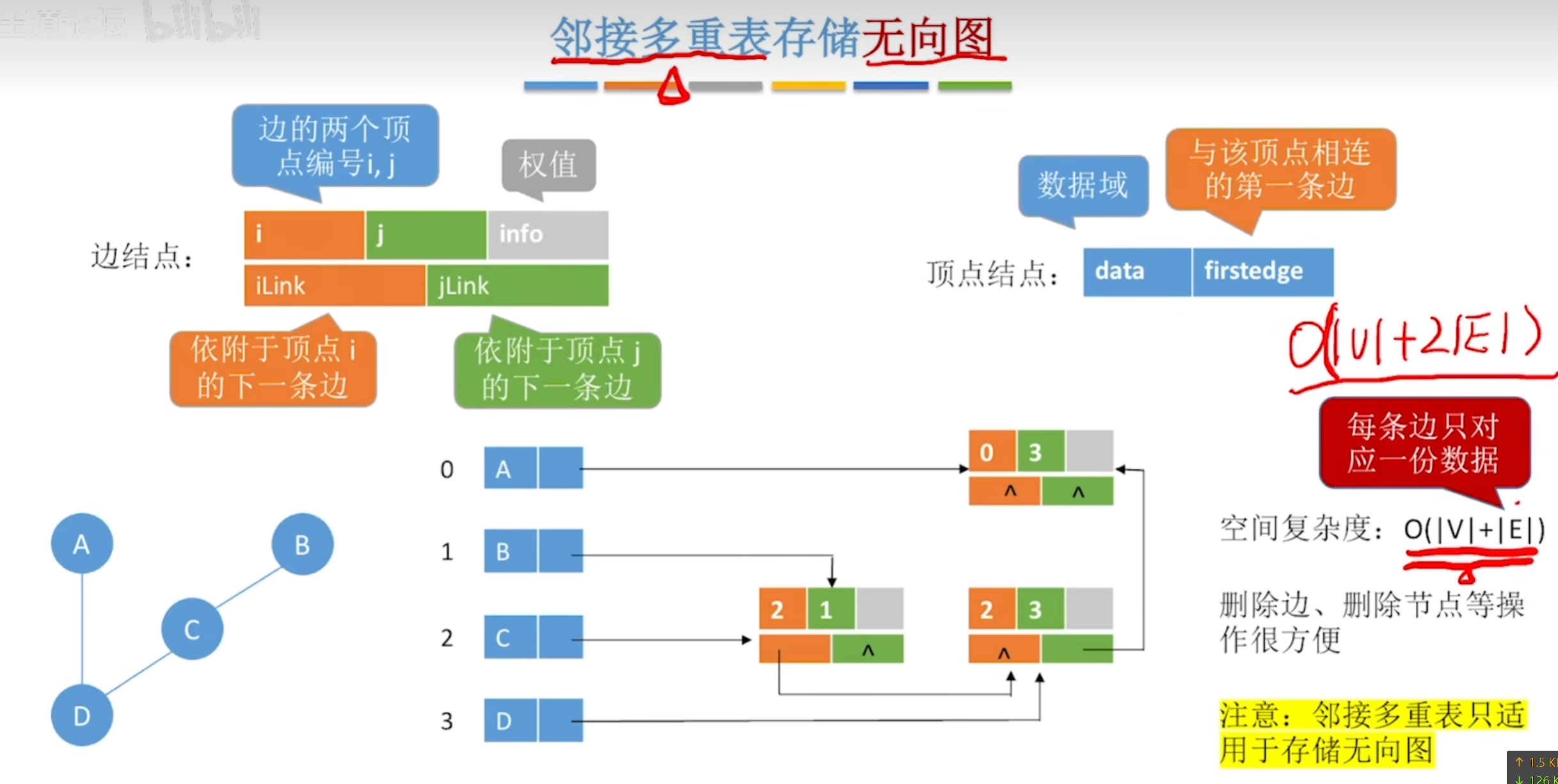
邻接多重表

邻接矩阵存储无向图的缺点：每条边对应两份冗余信息，删除顶点、删除边等操作时间复杂度高。

邻接表存储无向图的缺点：空间复杂度高。

图的基本操作

操作	邻接矩阵	领接表
判断是否存在边	$O(1)$	$O(1)-O(V)$
获取图G中边(x,y)或<x,y>对应的权值	$O(1)$	$O(1)-O(V)$
设置图G中边(x,y)或<x,y>对应的权值	$O(1)$	$O(1)-O(V)$
无向图列出图G中与结点x邻接的边	出$O(V)$	$O(1)-O(V)$
有向图列出图G中与结点x邻接的边	遍历矩阵一行一列$O(V)$	入：遍历所有顶点找连到这个顶点的。出$O(1)-O(V)$ 入$O(E)$
无向图插入顶点x	新增一行一列$O(1)$	加一个新结点$O(1)$

无向图删除顶点x	删除这一行和这一列，标记为已删除。$O(V)$	删除这一个结点和后面连的关系链，标记为已删除。$O(1)-O(E)$
有向图删除顶点x	删除这一行和这一列，标记为已删除。$O(V)$	删出边：删除这一个结点和后面连的关系链，标记为已删除。$O(1)-O(E)$ 删入边：删除这一个结点和后面连的关系链，标记为已删除。遍历所有顶点找到所有指向这个顶点的顶点删除。$O(E)$
无向图增加边	$O(1)$	$O(1)$
有向图增加边	$O(1)$	$O(1)$
无向图求图G中顶点x的第一个邻接点	$O(1)-O(V)$	$O(1)-O(V)$
有向图求图G中顶点x的第一个邻接点	$O(1)-O(V)$	出：$O(1)$ 入：$O(1)-O(E)$
无向图假设图G中顶点y是顶点x的一个邻接点，返回除y之外顶点x的下一个邻接点的顶点号，若y是x的最后邻接点，则返回-1	$O(1)-O(V)$	$O(1)$

图的遍历

	广度优先遍历（BFS）	深度优先遍历（DFS）
时间复杂度	矩阵：$O(n+e)$ 表：$O(n^2)$	矩阵：$O(n+e)$ 表：$O(n^2)$
空间复杂度	矩阵：$O(n)$ 表：$O(n)$	矩阵：$O(n)$ 表：$O(n)$
对应树中	层序遍历	先序遍历（根左右）
辅助数据结构	队列	栈
应用	单源最短路径	判断是否有环
🌳高	低	高

图的应用

最小生成树

各个算法

	Prim算法（加点法）	Kruskal算法（加边法）
步骤	从一个顶点开始构建生成树，依次将权值最小的顶点加入生成树，直到所有顶点都加入。	写出所有顶点，依次选择一条权值最小的边，使这条边的两头连通，直到所有结点都连通。
时间复杂度	$O(n^2)$	$O(Elog_2E)$

性质

边数小于 n-1，不存在最小生成树。边数等于 n-1，唯一为图本身。边数大于n-1，生成树不唯一。
若最小生成树不唯一，则一定存在权值相等的边。当图的各边的权值互不相等时，图的最小生成树是唯一的。
最小生成树可能不唯一，但代价一定相同。

最短路径问题

各个算法

	BFS算法	Dijkstra算法	Floyd算法
用途	单源最短路径	单源最短路径（也可以两顶点）	双源最短路径
无权图	适用	适用	适用
有权图	不适用	适用	适用
带负权图	不适用	不适用	适用
带负回路图	不适用	不适用	不适用
时间复杂度	$O(n^2)$或$O(n+E)$	$O(n^2)$	$O(n^3)$

BFS算法

	说明	V1	V3	V4	V5	V6	V7	V8	V9	V10
dist数组	最短路径长度
path数组	前驱节点

选择一个源节点，将其路径设为0，按广度优先顺序依次访问节点，修改路径长度为上一个节点+1，并将前驱节点填入。

Dijkstra算法

	说明	V1
Final数组	标记是否为最短路径	是
dist数组	最短路径长度	0
path数组	前驱节点	-1

选择一个源节点，标记final为是，然后在不是最短路径的里面找dist最小的，依次加到其余节点上，看是否比原来的值小，同时修改前驱。循环剩余不是最短路径的节点。

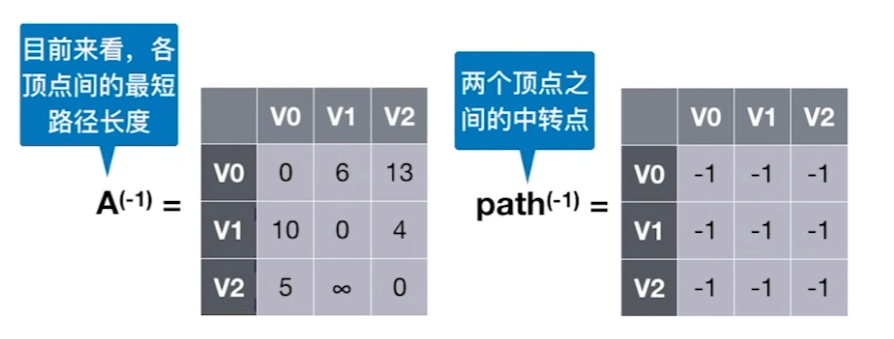
Floyd算法

A矩阵：行坐标通过某个点到列坐标的距离

path：行坐标到列坐标最短路径应该的前驱

写出不通过任何点两两点之间的距离，依次通过前一个表判断从各个点中转的距离，判断是否比原来的值小，如果小的话，更新最短路径并更新最短路径前驱。

性质

求解最短路径允许有环路的出现。

有向无环图描述表达式

写出不重复的各个节点
按运算顺序为运算符编上序号
➕同层，✖️上层

拓扑排序

拓扑排序求法

依次找到入度为零的点，写出来之后删掉这个点和边。

性质

对于任一有向图，若它的邻接矩阵为上三角或下三角，则一定存在拓扑序列（可能不唯一）。反之，若图存在拓扑序列，却不一定能满足邻接矩阵中主对角线以下的元素均为零，但是可以通过适当地调整结点编号，使其邻接矩阵满足前述性质。
在拓扑排序算法中为暂存入度为零的顶点，可以使用栈，也可以使用队列，因为顺序随便。

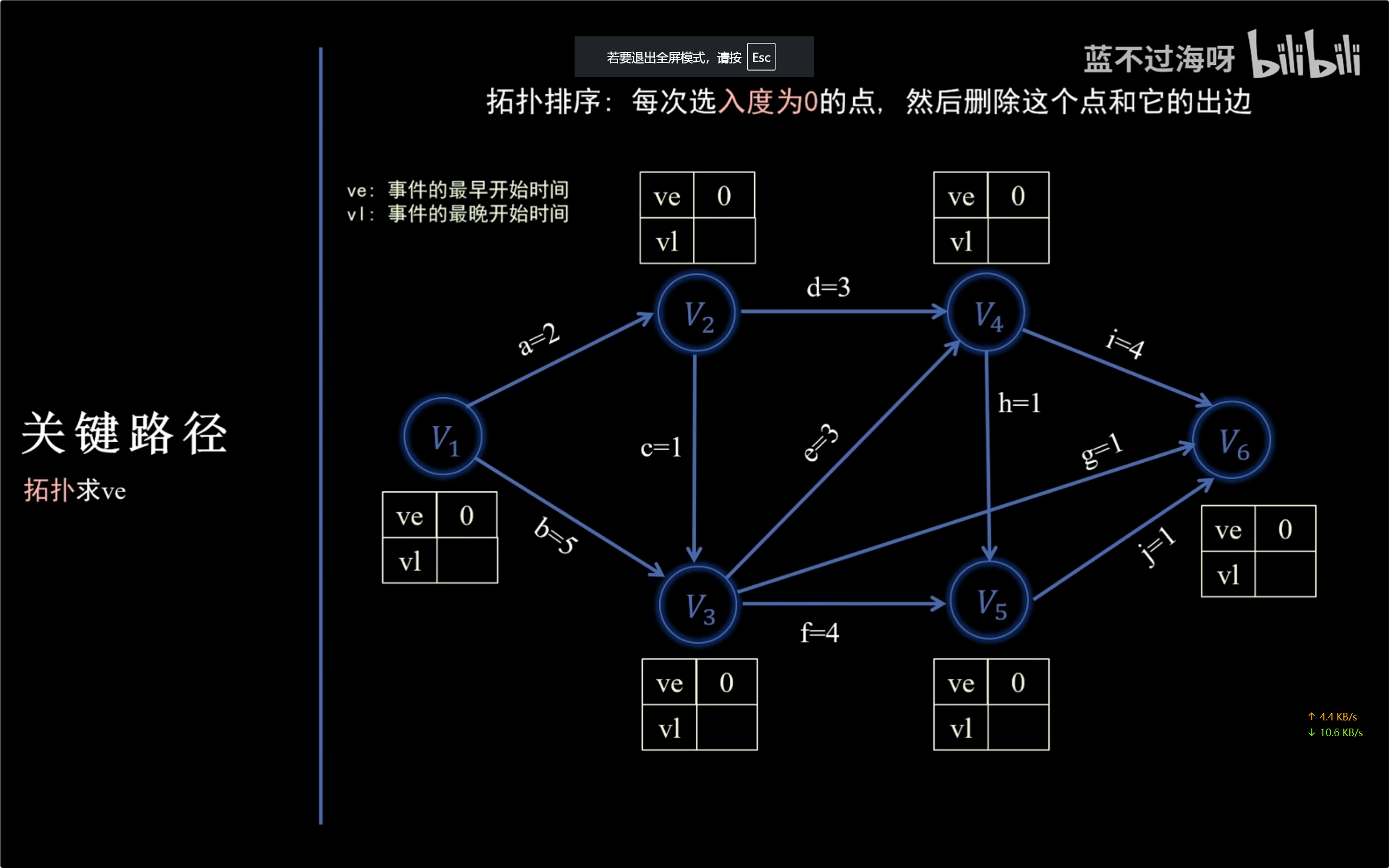
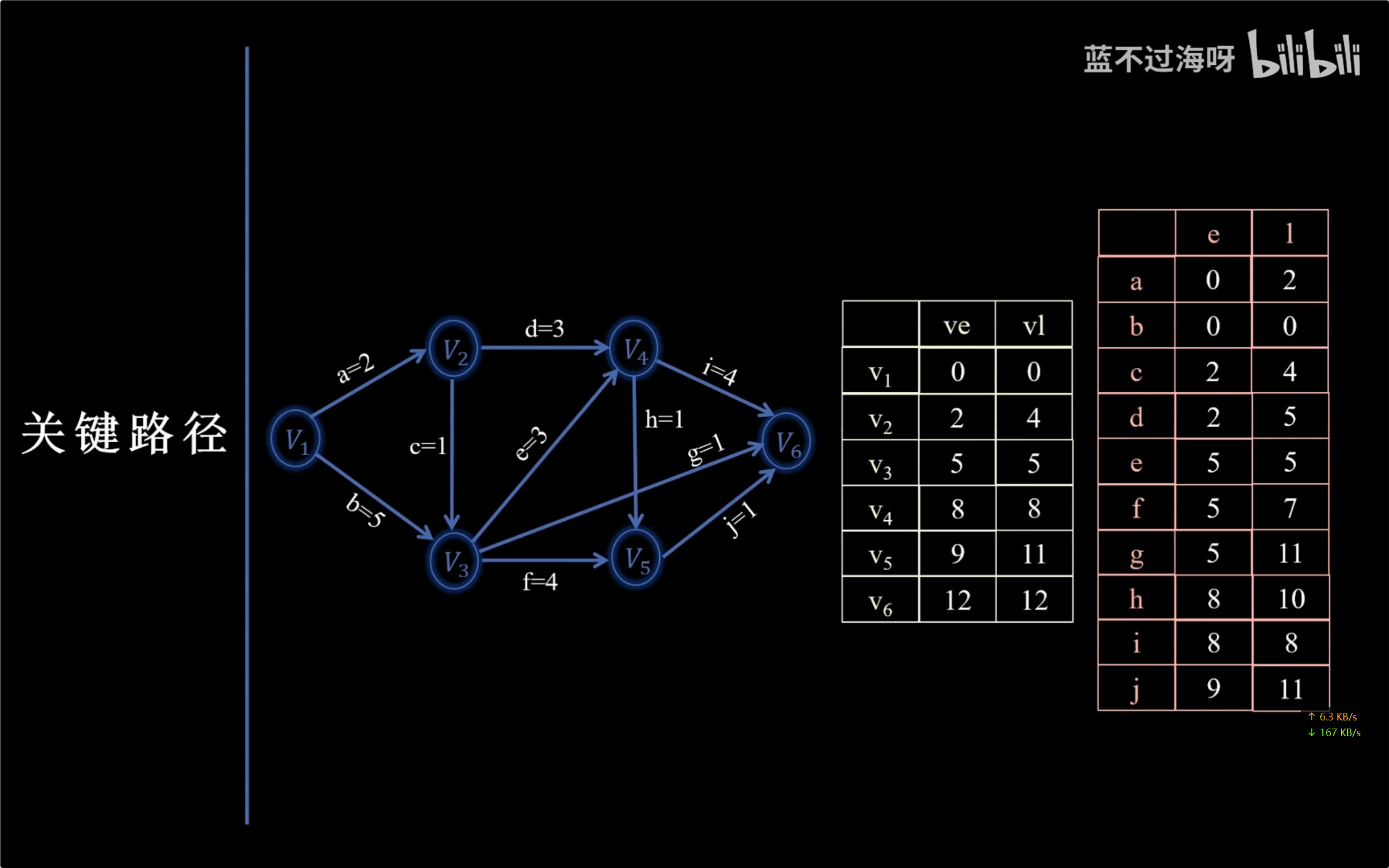
AOE网和关键路径

关键路径的求法

AOE网是一个【有向无环图】，关键路径也就是最长路径。

【图-AOE网和关键路径】 https://www.bilibili.com/video/BV1dy421a7S1?t=659.3

先求点：正向拓扑排序找最大的是最早开始时间，再逆向逆拓扑排序找最小的是最晚开始时间。

再求边：边最早就是边起点最早，边最晚就是边终点最晚减边耗时。

最早和最晚时间一样的是关键路径。

性质

改变所有关键路径的公共部分不一定影响关键路径，只有缩短才会缩短工期。
关键路径上的活动延长多少，工期就随之延长多少。

查找

基本概念

平均查找长度

查找概率✖️查找次数

线性结构

	要求	时间复杂度	ASL
顺序查找			$\frac{n+1}{2}$（一般） $\frac{n}{2}+\frac{n}{n+1}$（有序）
折半查找	必须是数组必须有序	$O(log_2n)$	$log_2(n+1)-1$

折半查找

性能分析

查找成功的平均查找长度：$((n+1)/n)*(log(n+1)-1)$

查找失败的最多比较次数：${\lceil}log_2(n+1)\rceil$

查找失败的最少比较次数：${\lceil}log_2(n+1)\rceil-1$因为平衡二叉树最多相差1

注意点

表必须有序而且必须是顺序存储结构

二叉判定树

二叉判定树是用来分析折半查找而设计的二叉树

二叉判定树是一颗平衡二叉树
二叉判定树的最高度是${\lceil}log_2(n+1)\rceil$
向下取整左多等、向上取整左少等
有n个非叶节点和n+1个方形虚拟节点

分块查找

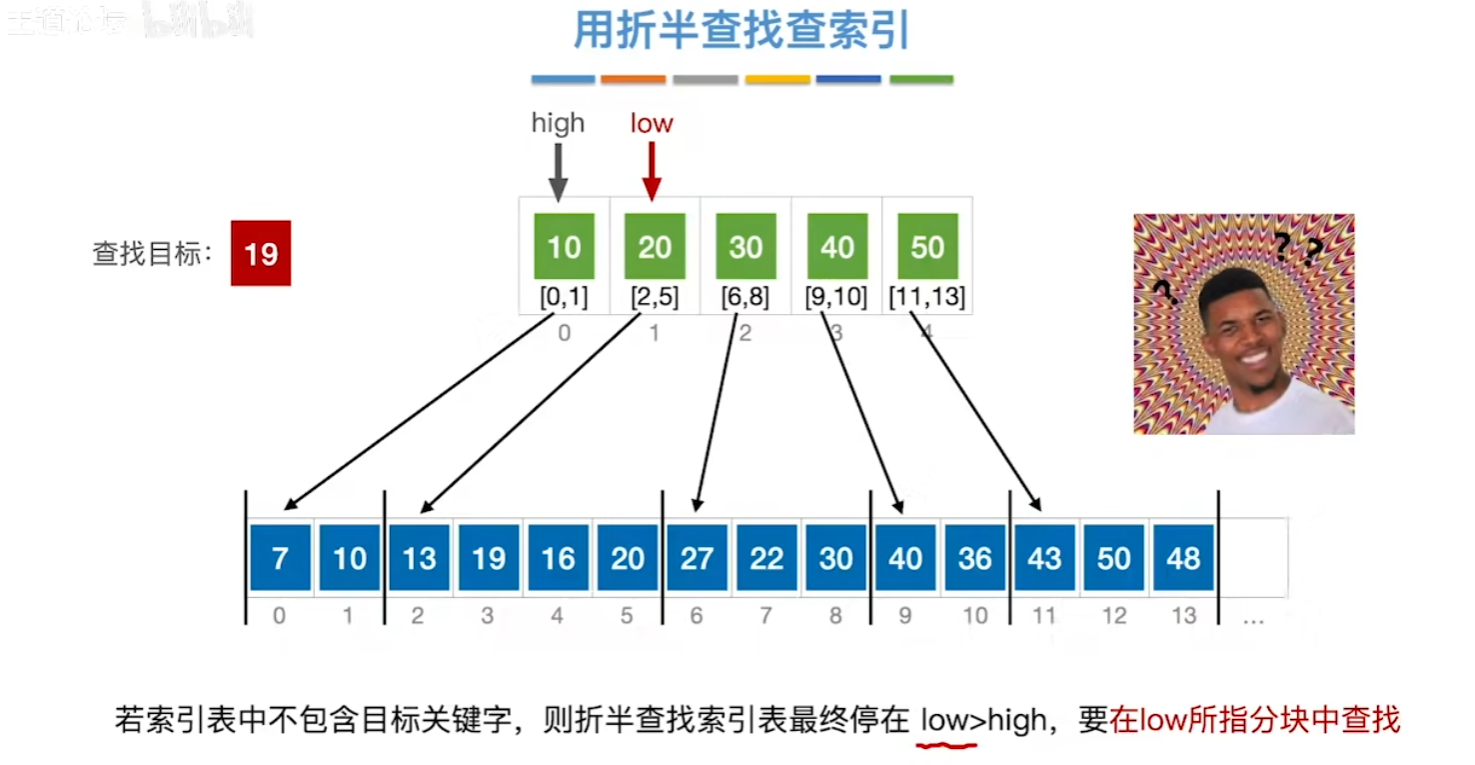
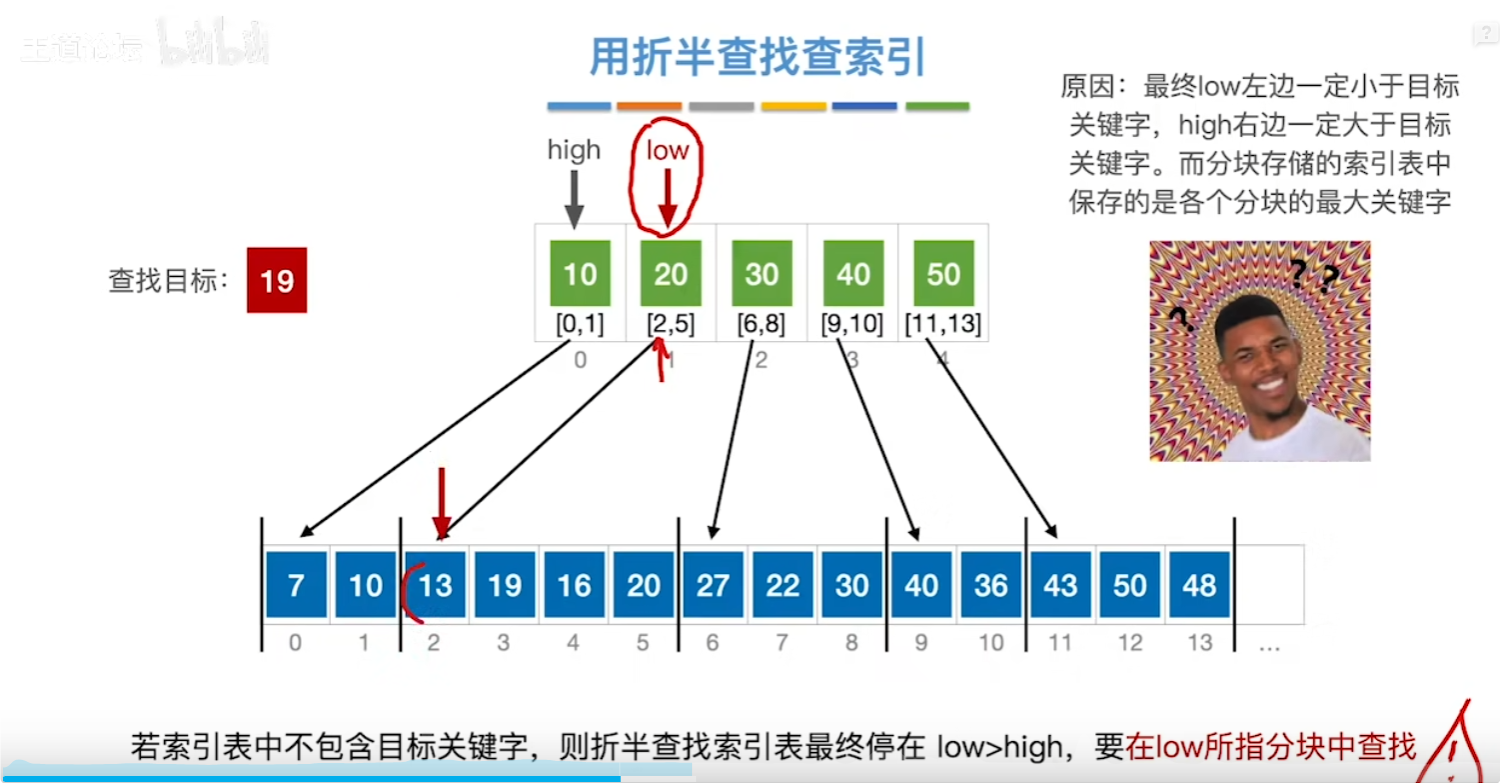
易错点

对索引表进行折半查找时，若索引表中不包含目标关键字，则折半查找最终停在low>high，要在low所指分块中查找。

查找效率分析

查索引	查块内	查索引	查块内	ASL=查索引➕查分块
顺序	顺序	$\frac{b+1}{2}$	$\frac{s+1}{2}$	$ASL=\frac{b+1}{2}+\frac{s+1}{2}=\frac{s^2+2s+n}{2s},当s=\sqrt{n}时,ASL_{min}=\sqrt{n}+1$
折半	顺序	${\lceil}log_2(b+1)\rceil$	$\frac{s+1}{2}$	$ASL={\lceil}log_2(b+1)\rceil+\frac{s+1}{2}$

树形结构

二叉排序树（BST）（二叉搜索树、二叉查找树）

二叉排序树的删除

删除	删除操作
叶子节点	直接删除
有左子树	删除后将其左子树接到上一层
有右子树	删除后将其右子树接到上一层
有左右子树	删除后将其左子树最大或右子树最小接到上一层

二叉排序树效率

平衡二叉树VS红黑树

旋转次数

树	插入	删除
AVL	最多两次(双旋)	最多树高($log_2n$)次
红黑树	最多两次(双旋)	最多三次

性能分析

树	查找效率	插入效率	删除效率
平衡二叉树	$O(log_2n)$	$O(log_2n)$	$O(log_2n)$
红黑树	$O(log_2n)$	$O(log_2n)$	$O(log_2n)$

树高就是查询效率，因此AVL的查询效率往往更优

平衡二叉树（AVL）

平衡因子

左子树高度-右子树高度的绝对值小于1，平衡因子均为1，即平衡二叉树满足平衡的最少结点情况

性质

当按关键字有序的顺序插入初始为空的平衡二叉树时，若关键字个数$n=2^k-1$时，则该平衡二叉树一定是一棵满二叉树。

深度为i的平衡二叉树最少有多少个结点？

公式：$ 对于 n \geq 3，有f(n) = f(n-1) + f(n-2) + 1 ，且f(1)=1和f(2)=2$

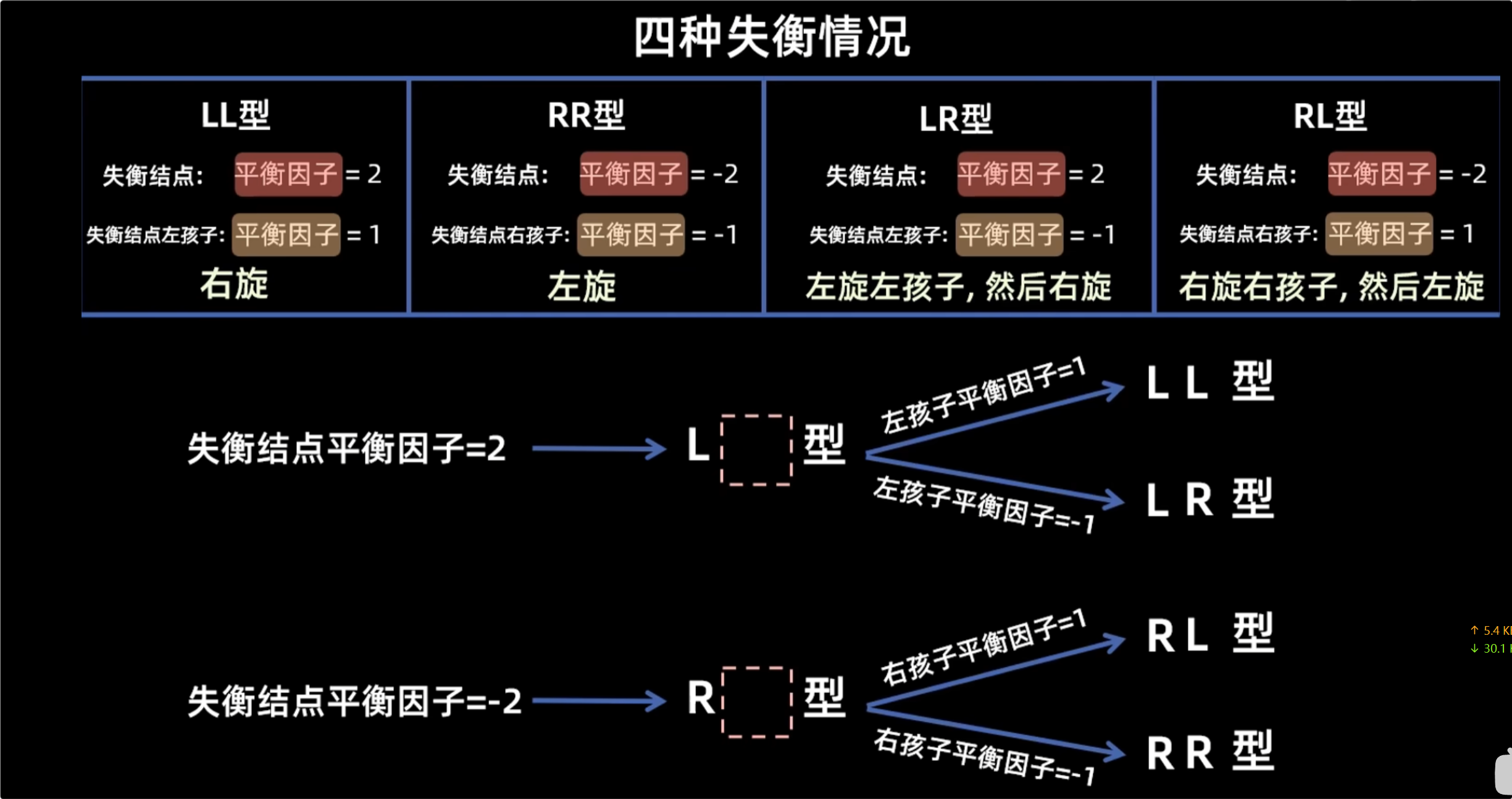
插入操作

红黑树

性质


左根右	二叉排序树（不一定要平衡）
根叶黑	根节点和叶子节点都是黑色
不红红	没有连续的两个红色节点
黑路同	任意节点到叶子节点路径上黑色节点数量相同

红黑树的红结点数最大可以是黑结点数的2倍。
红黑树的任意一个结点的左右子树高度(含叶结点)之比不超过2。
若所有节点都是黑色的，那么他一定是一颗满二叉树（黑路同，故路都是相同节点）
一棵含有n个结点的红黑树的高度至多为$2log_2(n +1)$

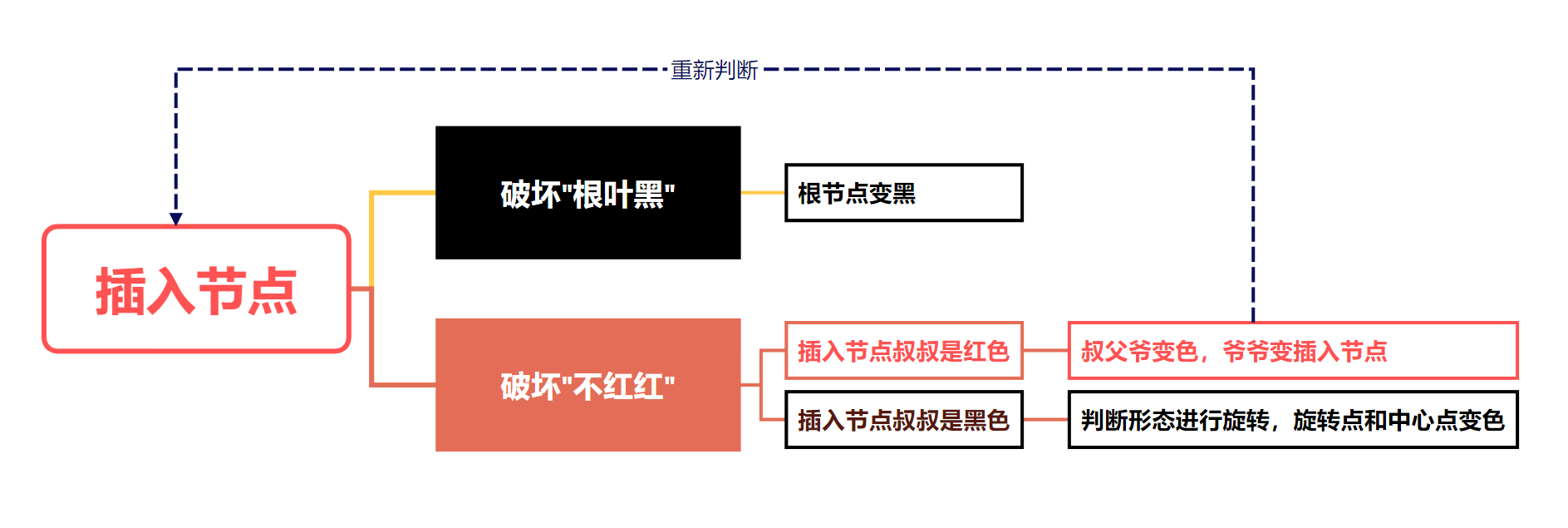
插入操作

二叉树的演变

考研, 华美数据结构

数据结构考研算法 C语言

本文由作者按照 CC BY 4.0 进行授权

栈

括号匹配

中缀转后缀机算

数组和特殊矩阵

对称矩阵

三角矩阵

三对角矩阵

树和二叉树

树的性质

二叉树

线索二叉树

图

无向图

有向图

简单图

子图

邻接矩阵法

领接表

十字链表

邻接多重表

图的基本操作

图的遍历

图的应用

最小生成树

各个算法

性质

最短路径问题

各个算法

性质

有向无环图描述表达式

拓扑排序

拓扑排序求法

性质

AOE网和关键路径

关键路径的求法

性质

查找

基本概念

平均查找长度

线性结构

折半查找

性能分析

注意点

二叉判定树

分块查找

易错点

查找效率分析

树形结构

二叉排序树（BST）（二叉搜索树、二叉查找树）

二叉排序树的删除

二叉排序树效率

平衡二叉树VS红黑树

旋转次数

性能分析

平衡二叉树（AVL）

平衡因子

性质

插入操作

红黑树

性质

插入操作

热门标签