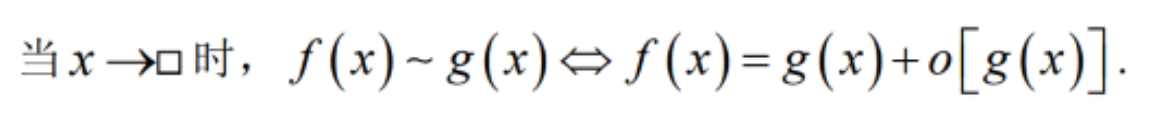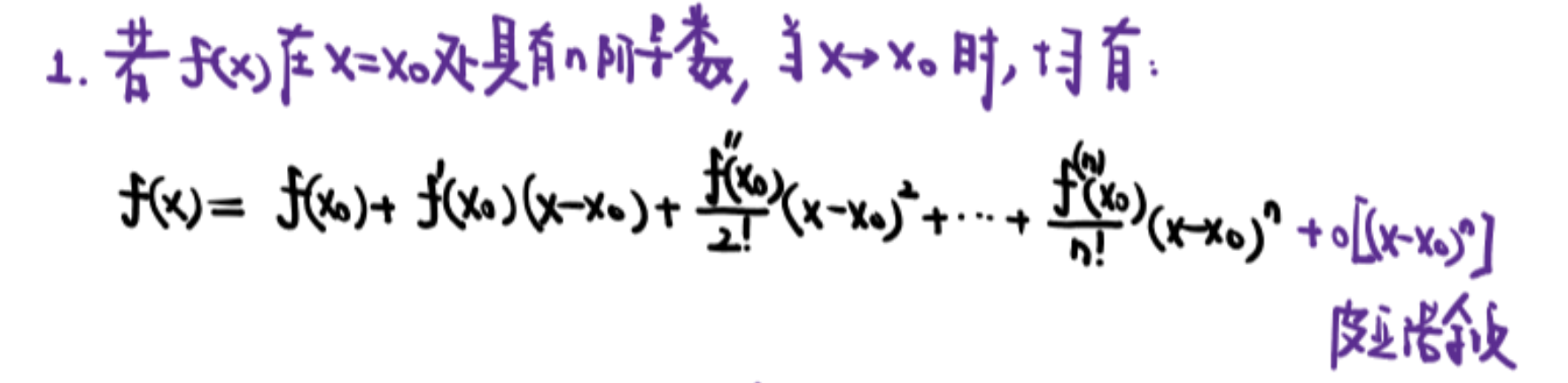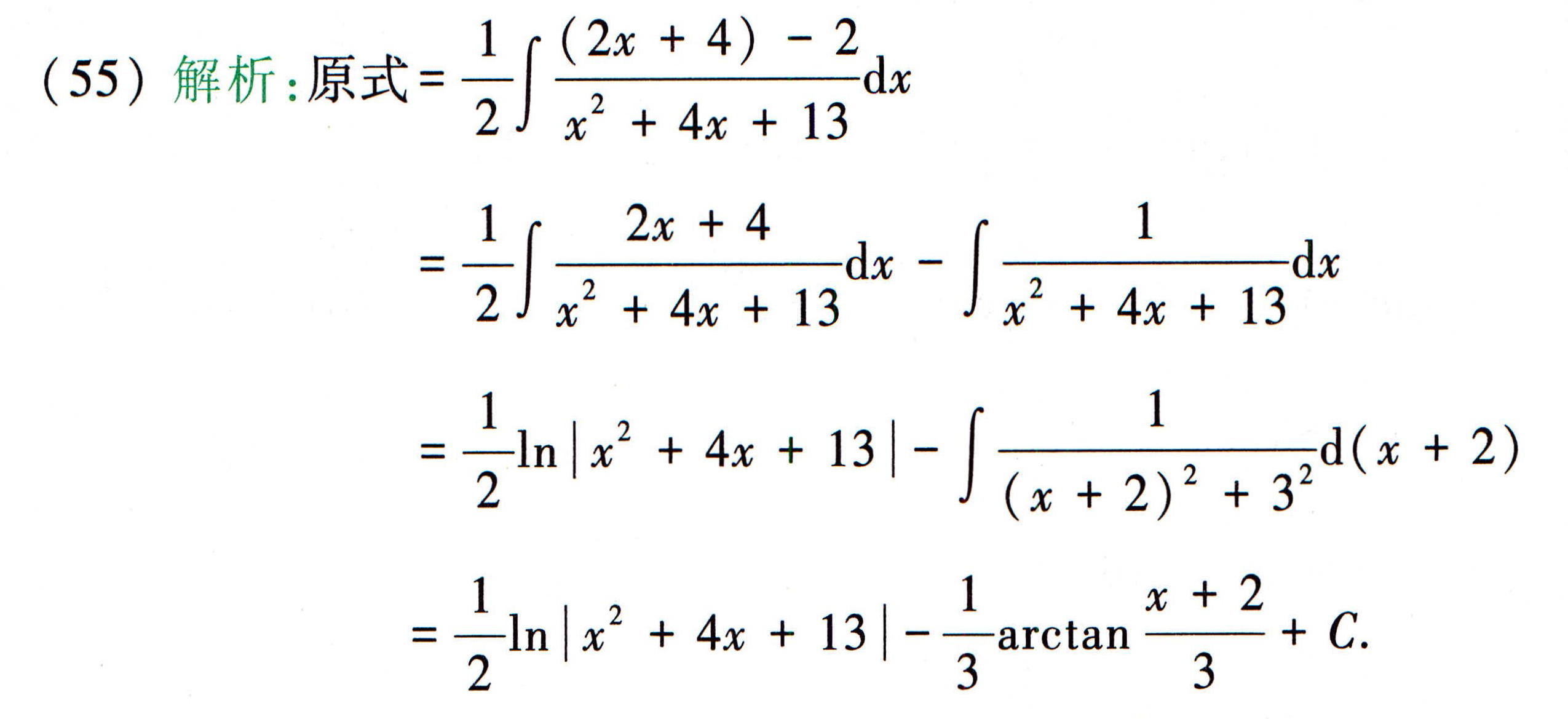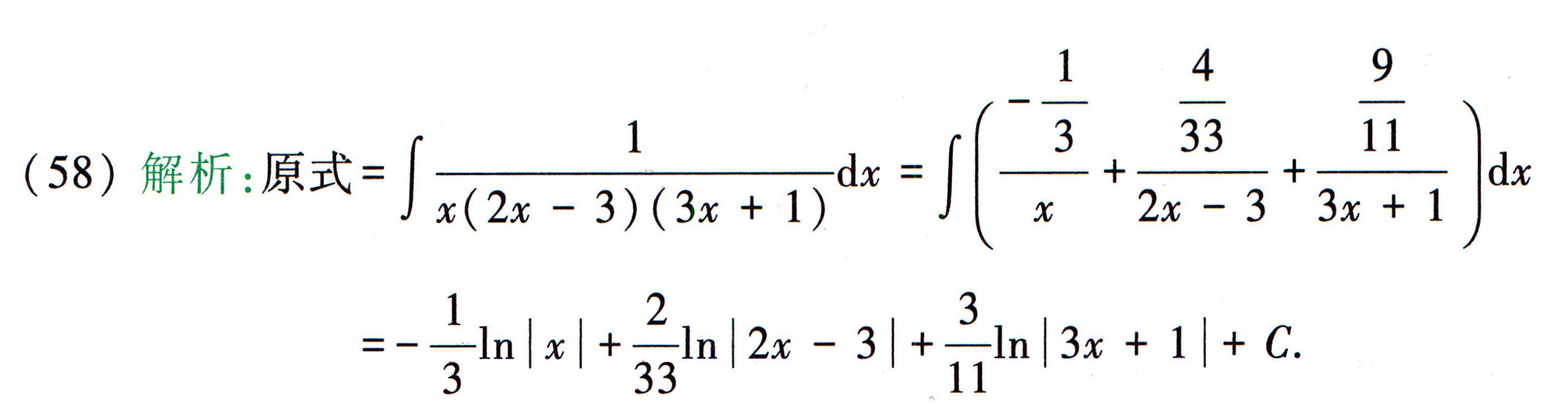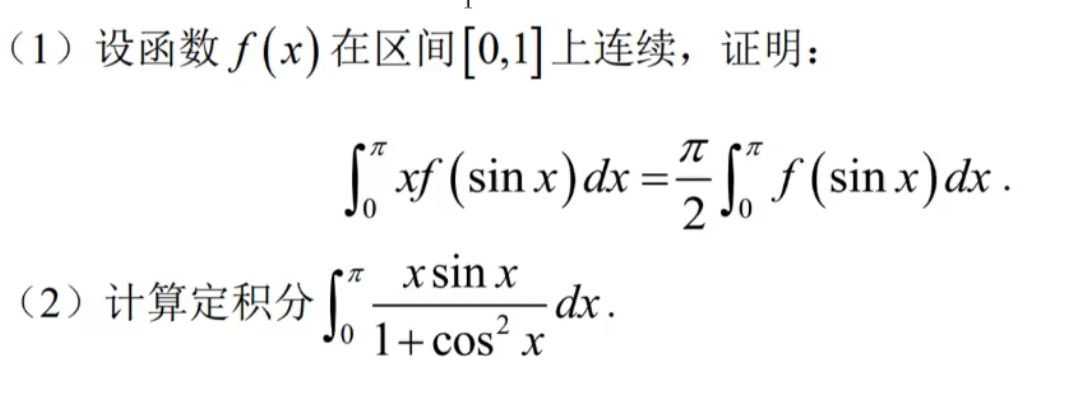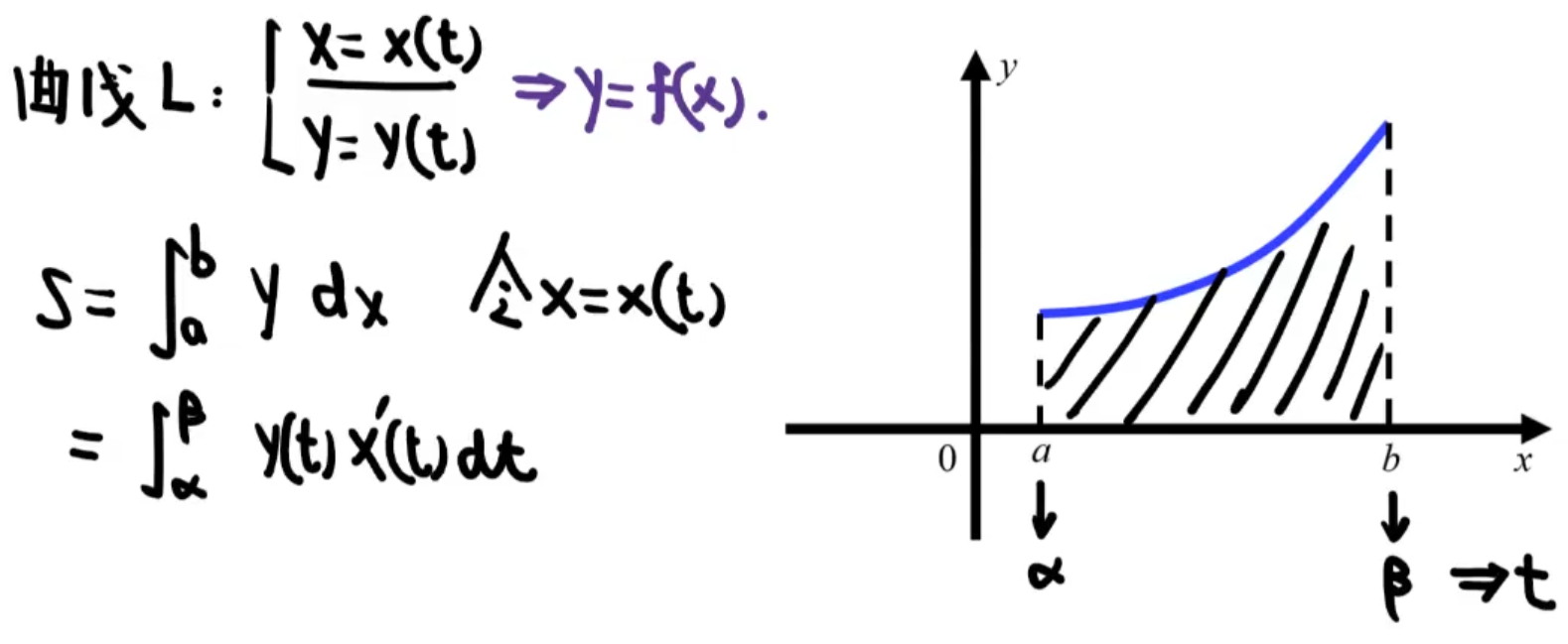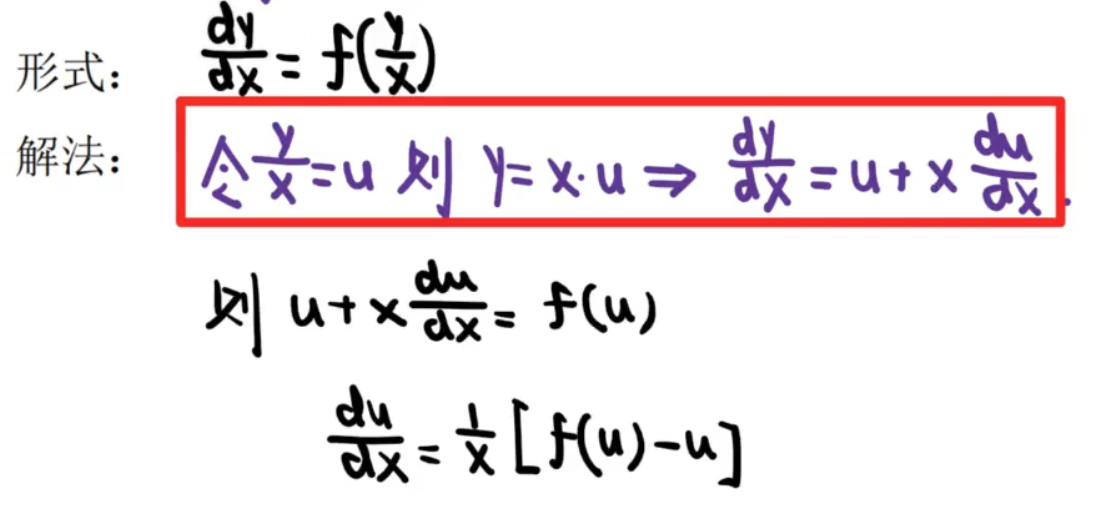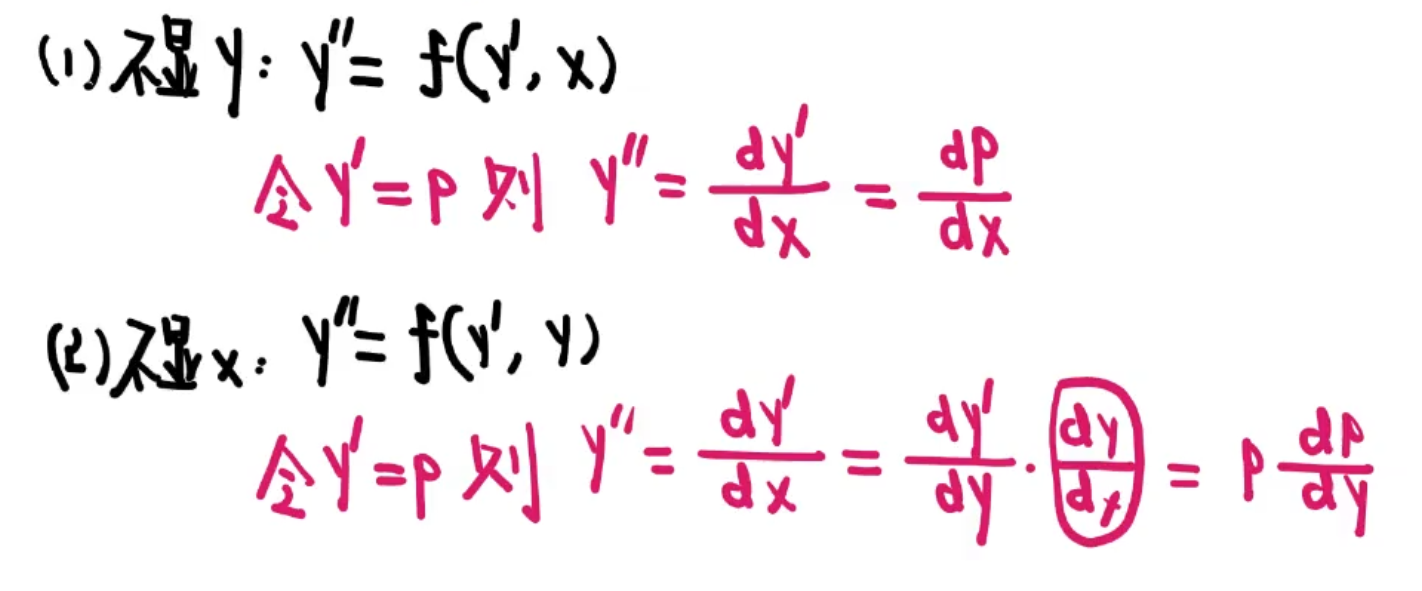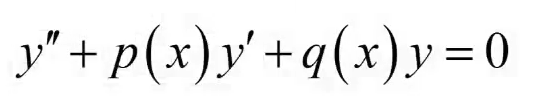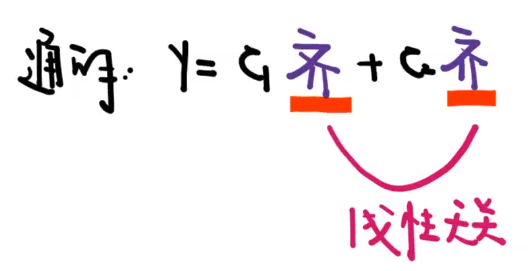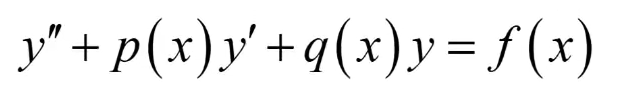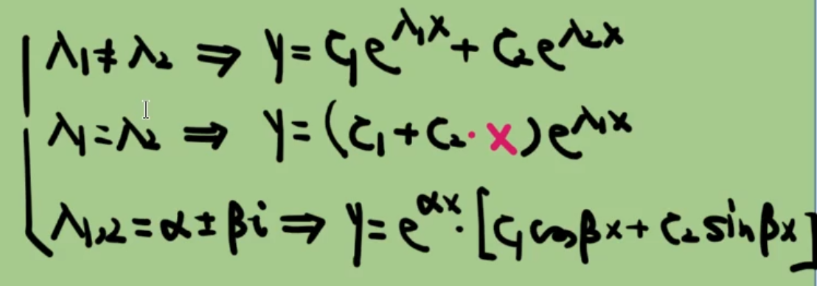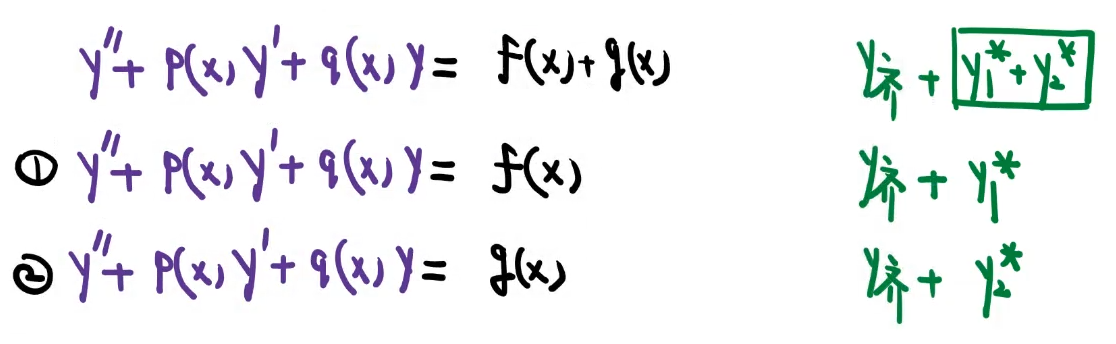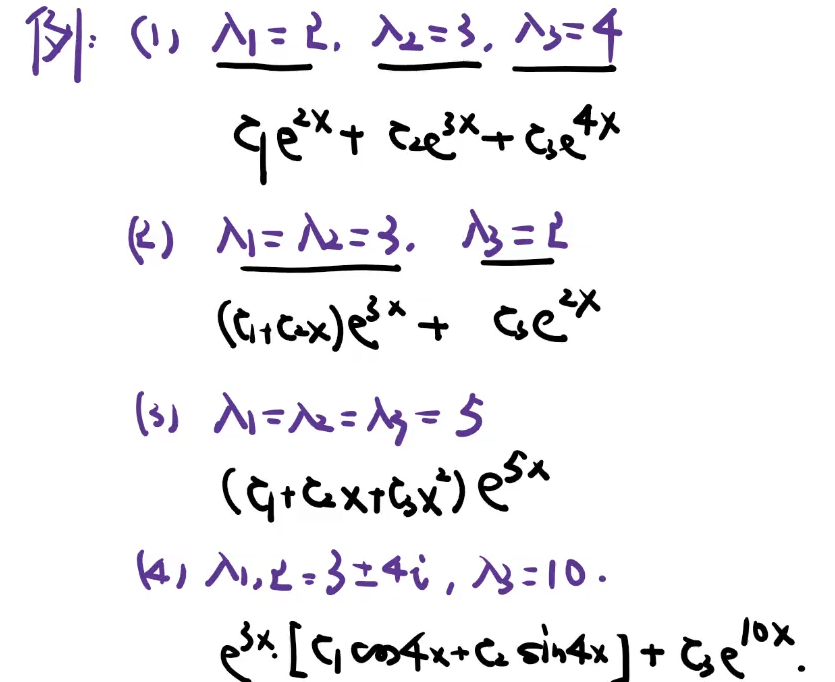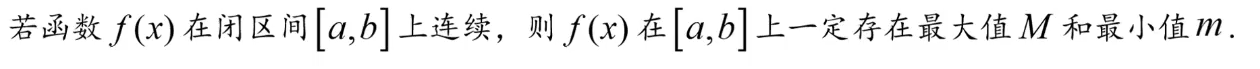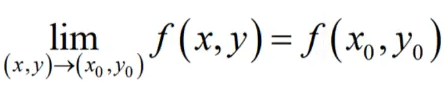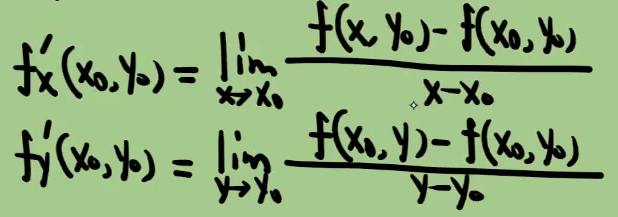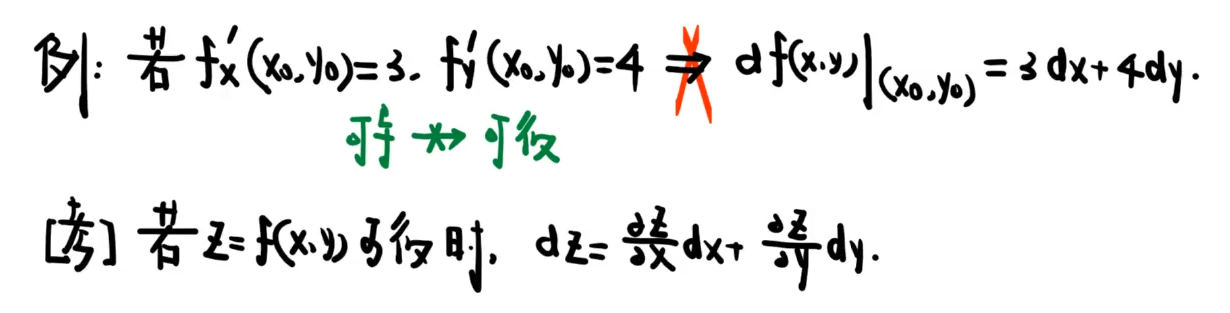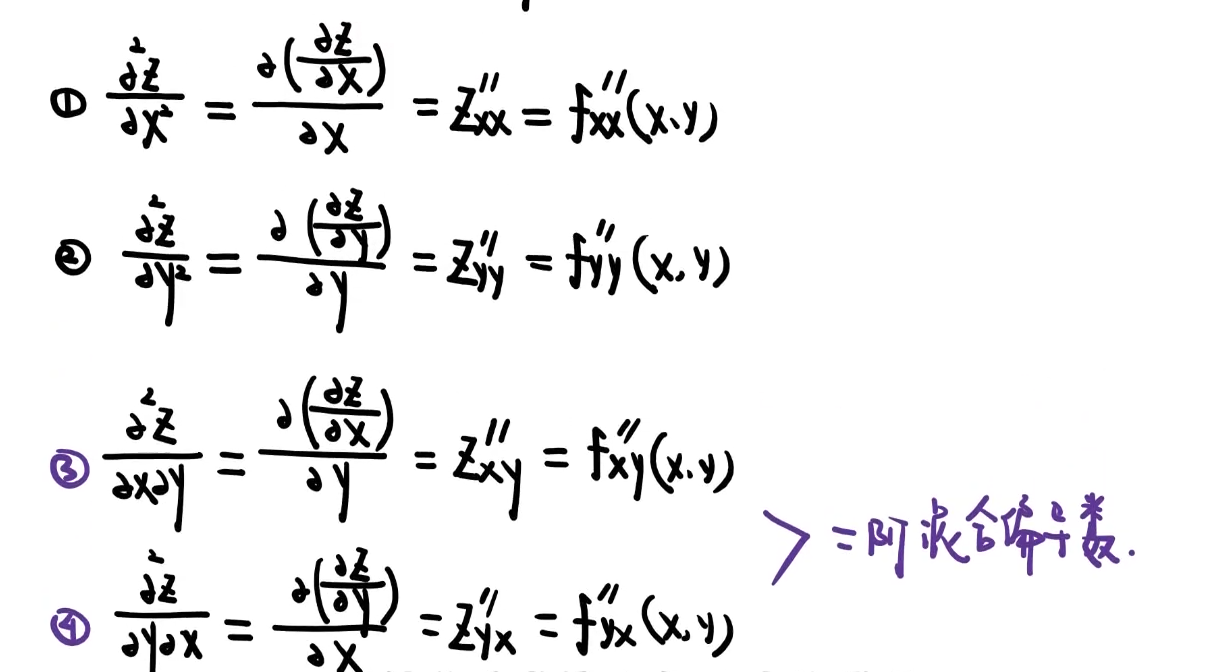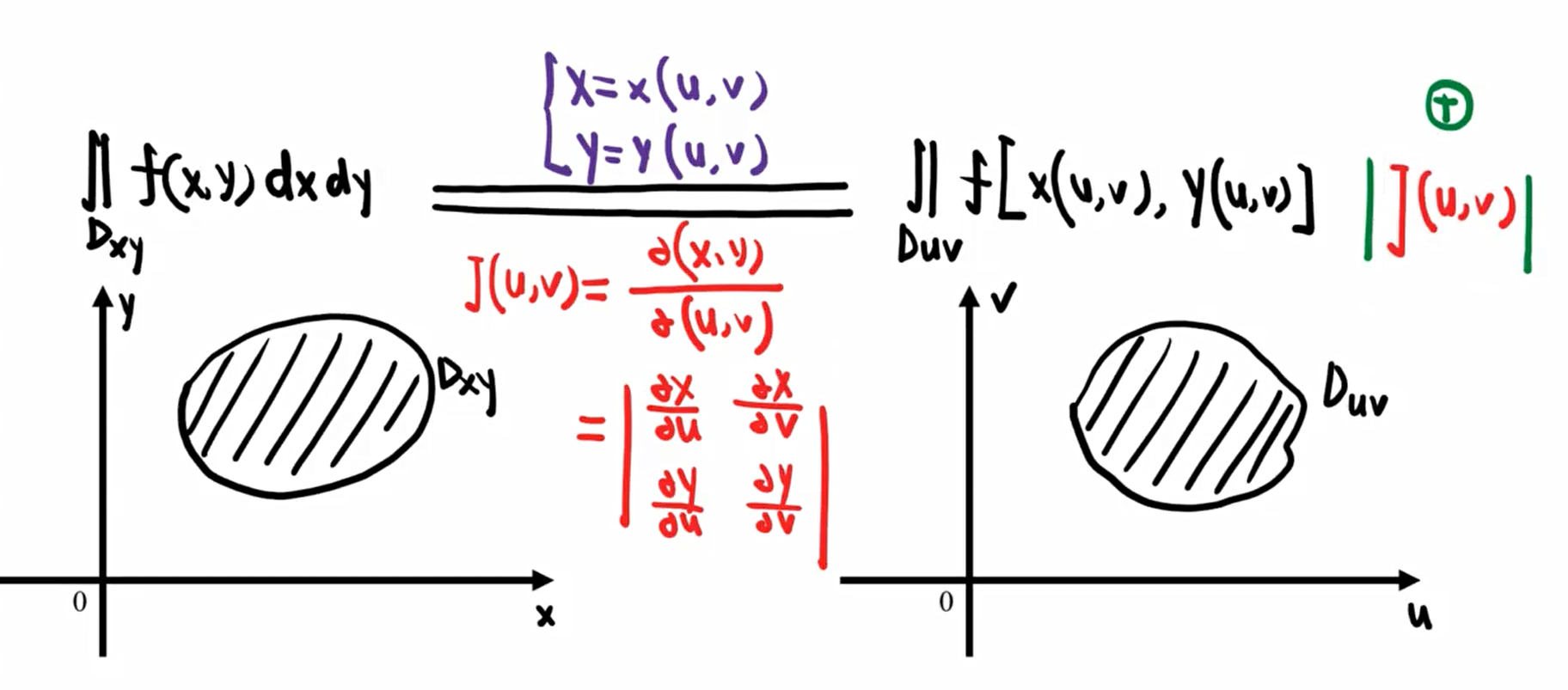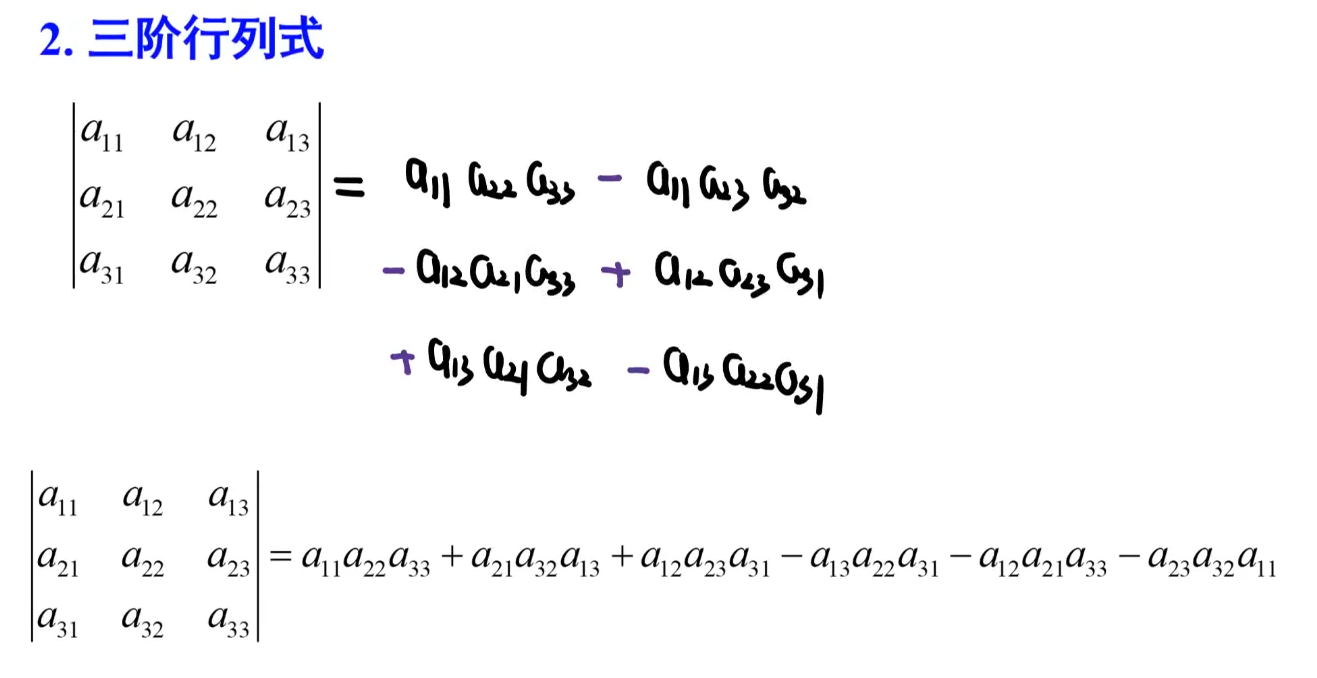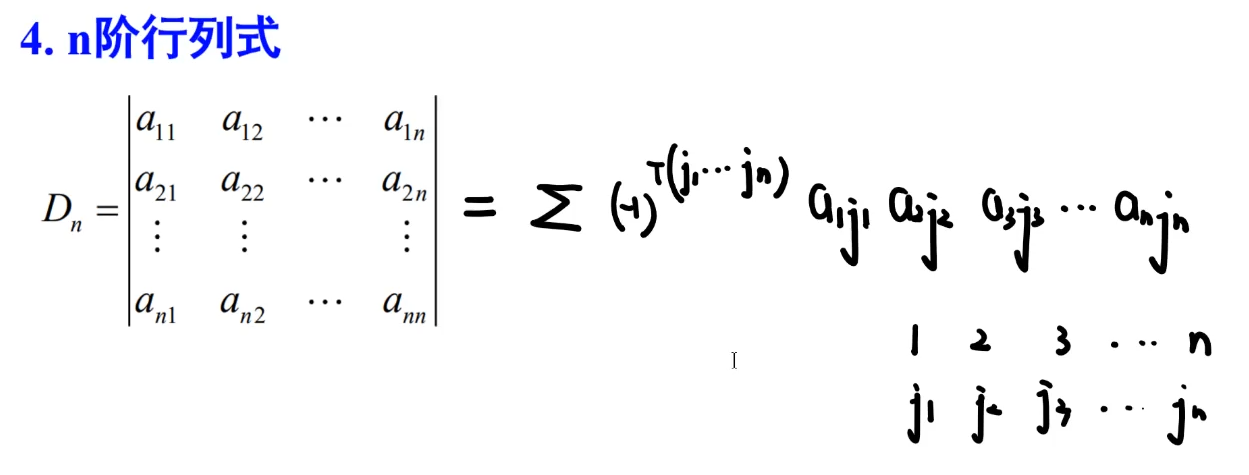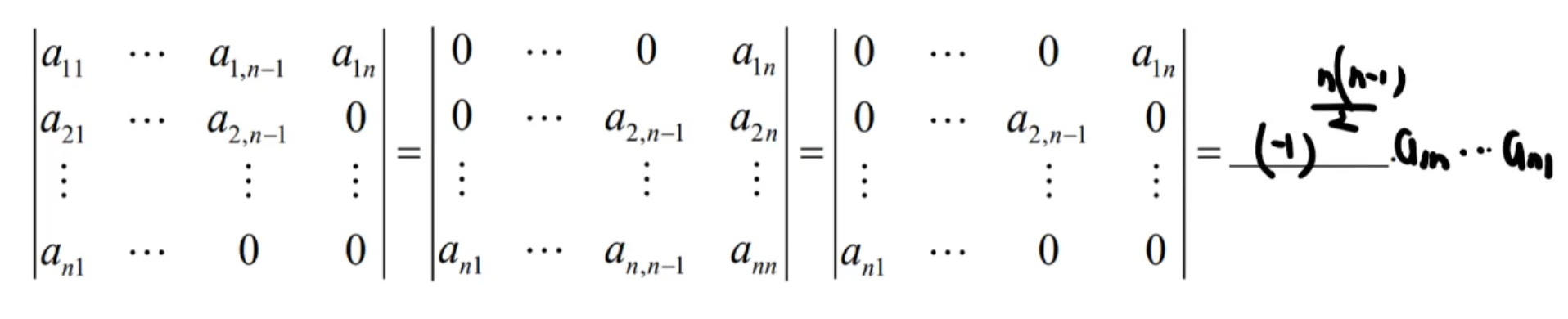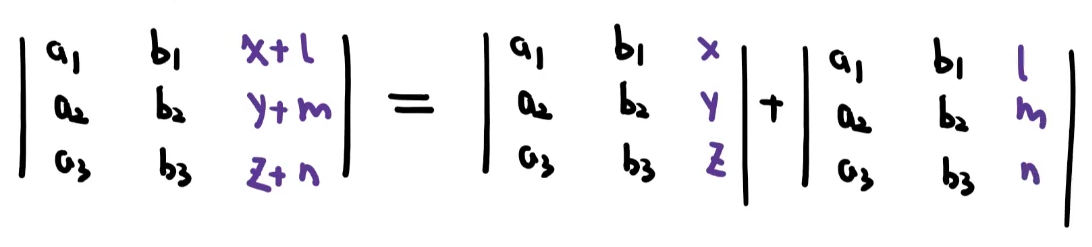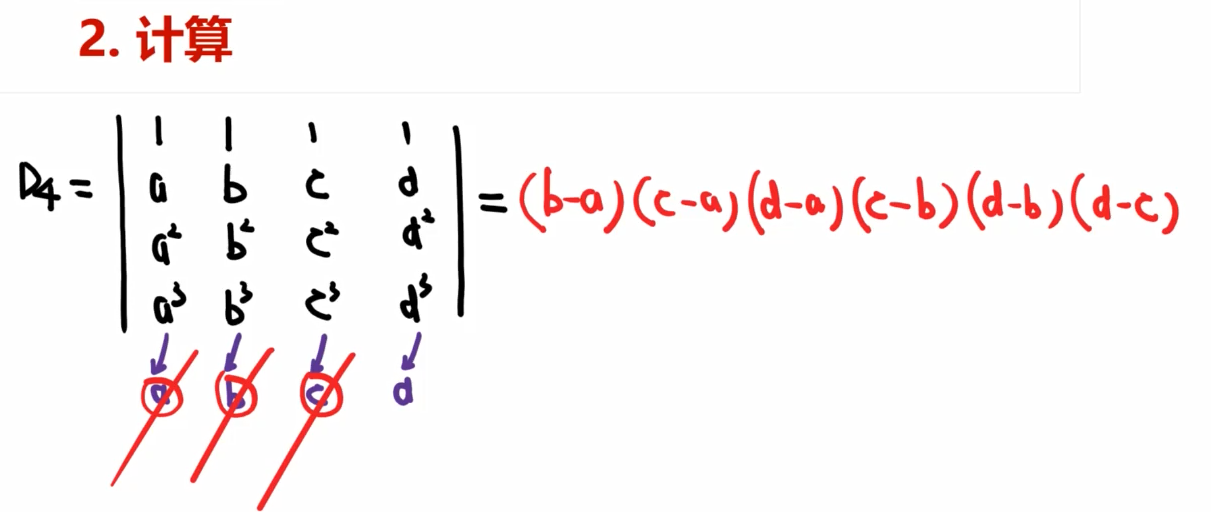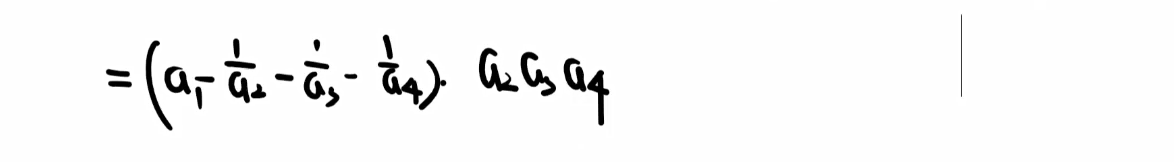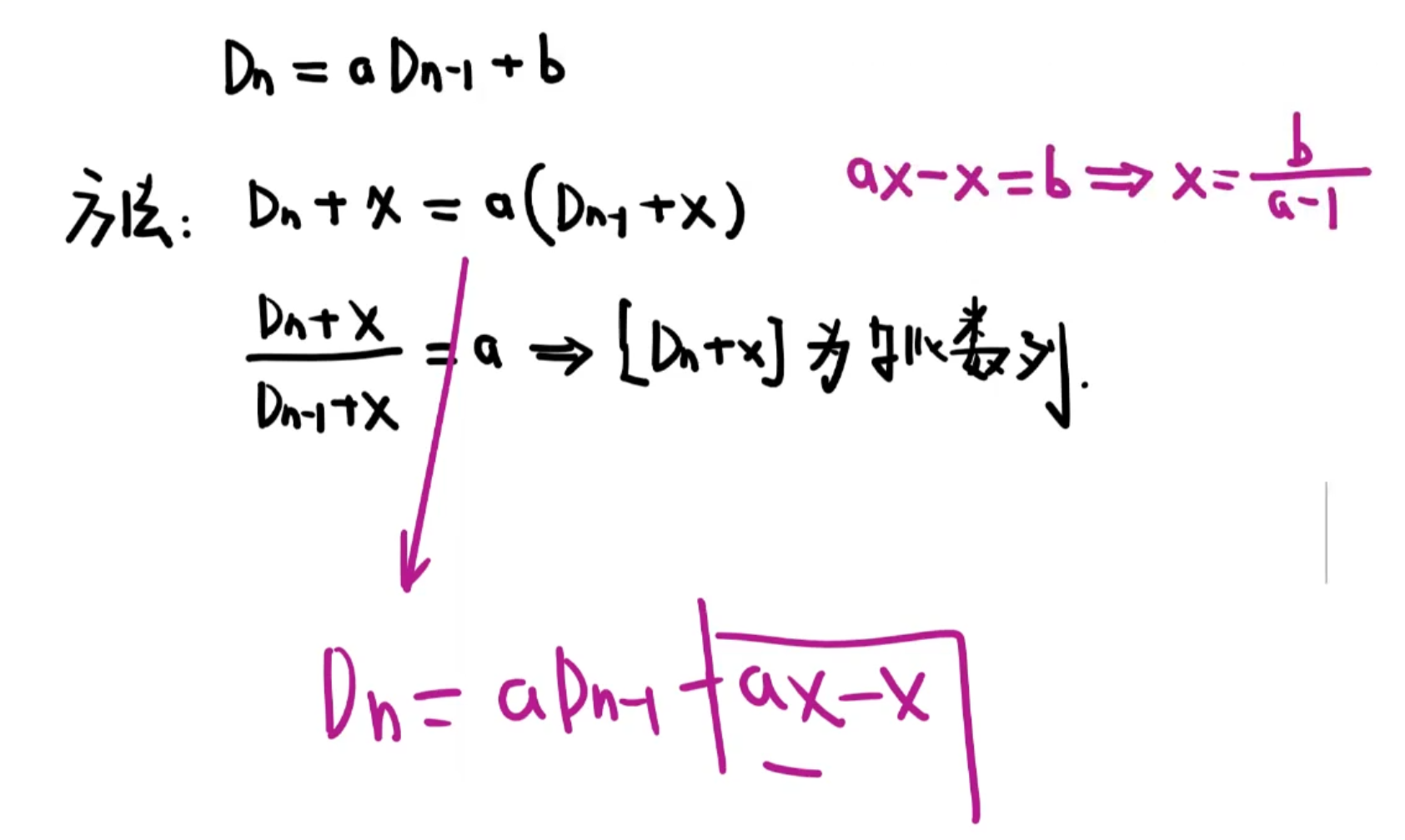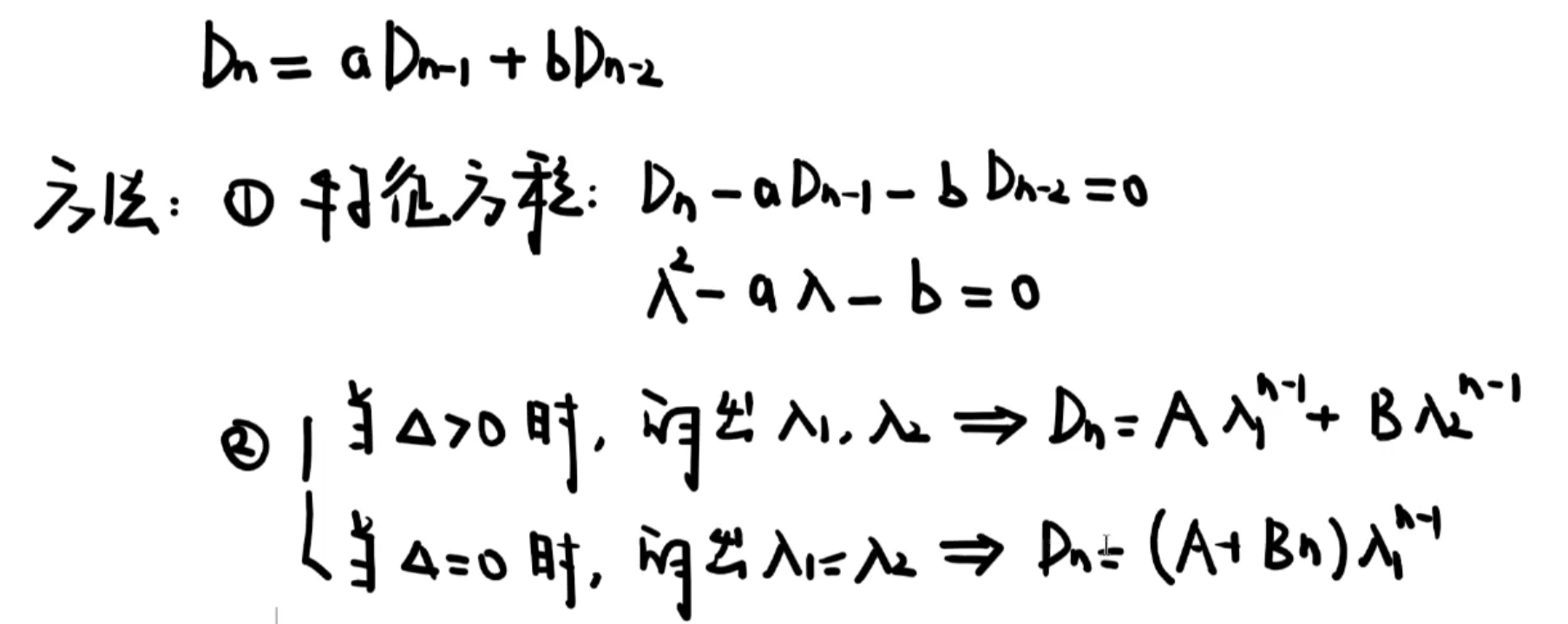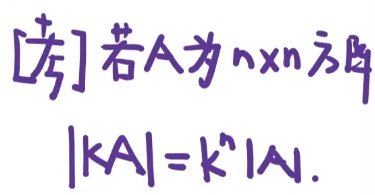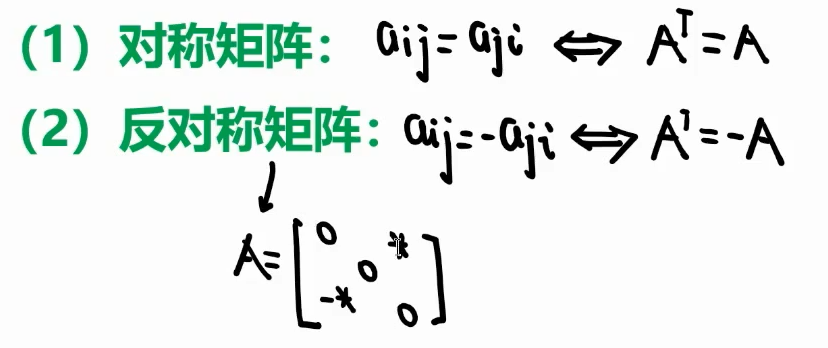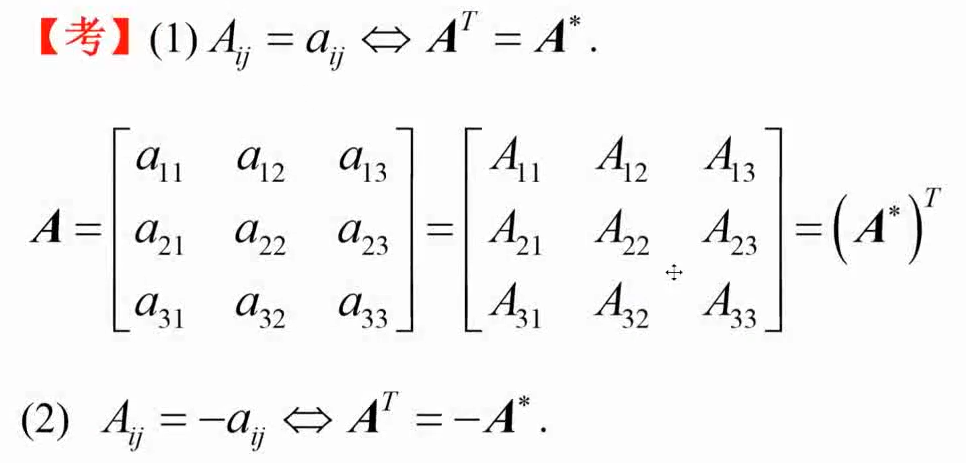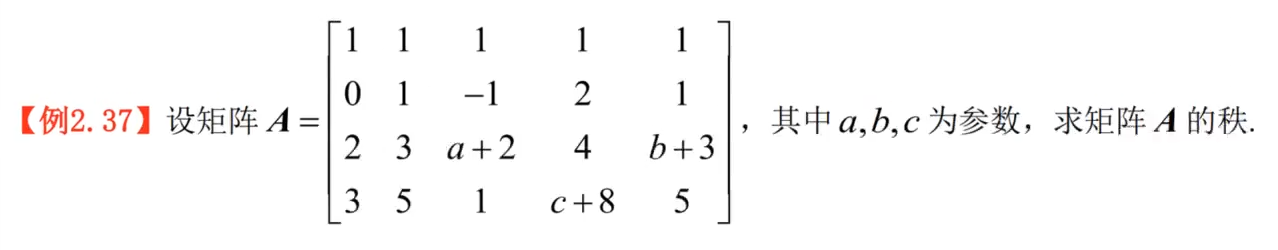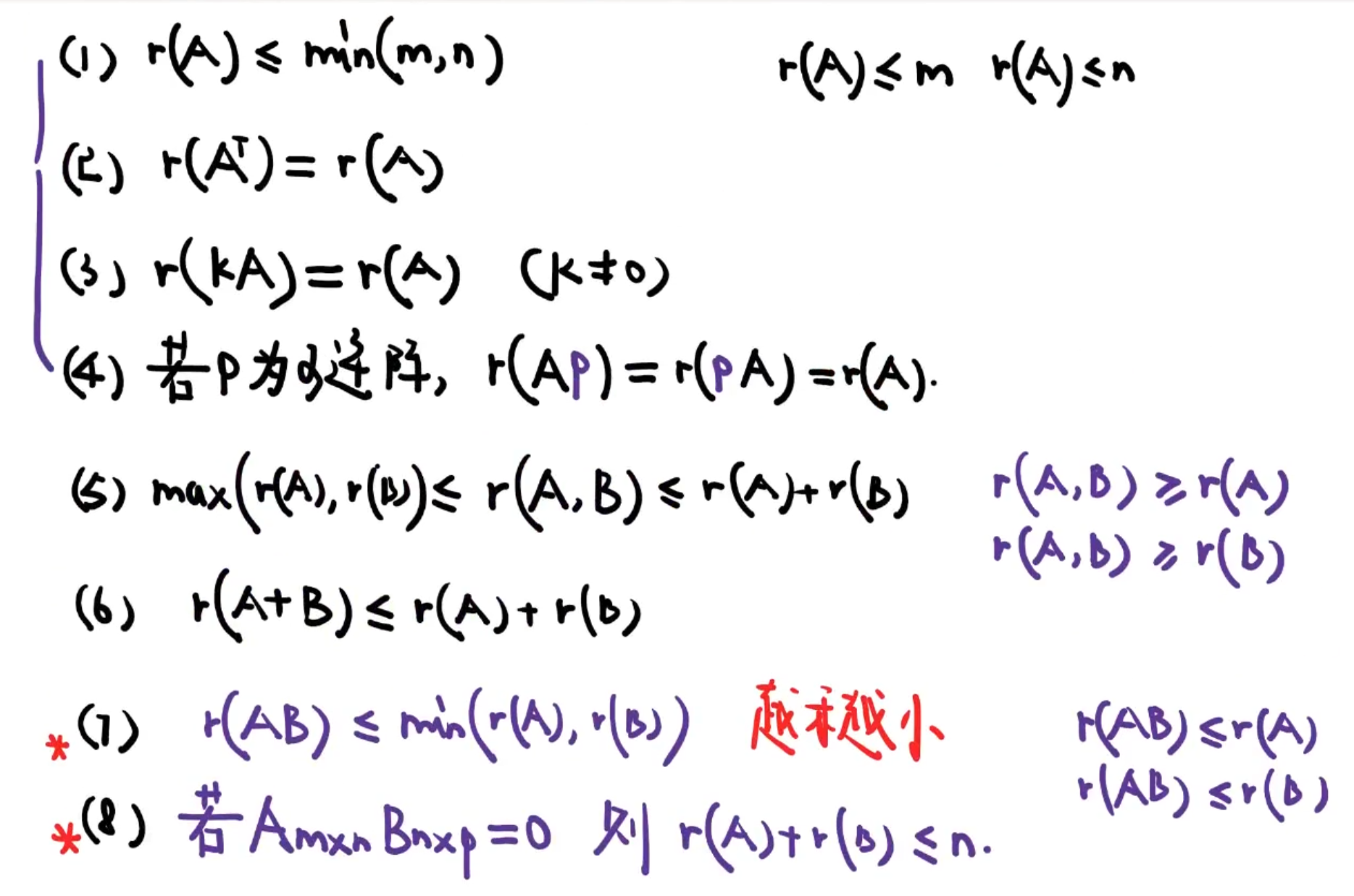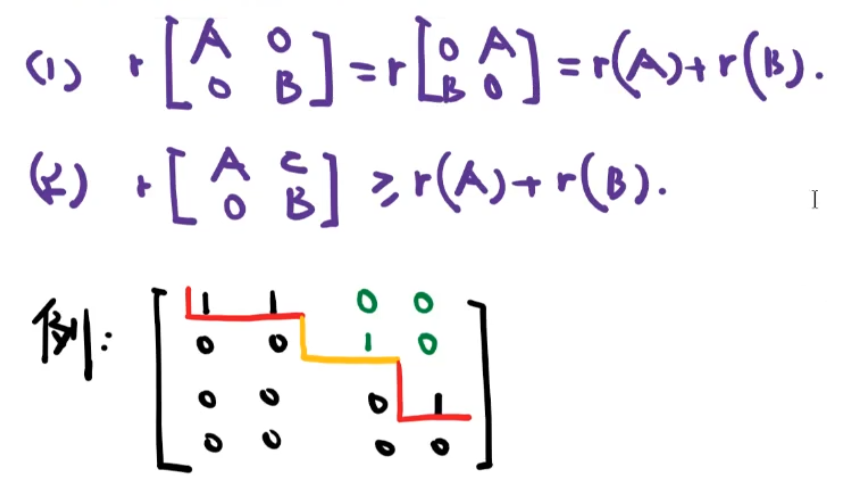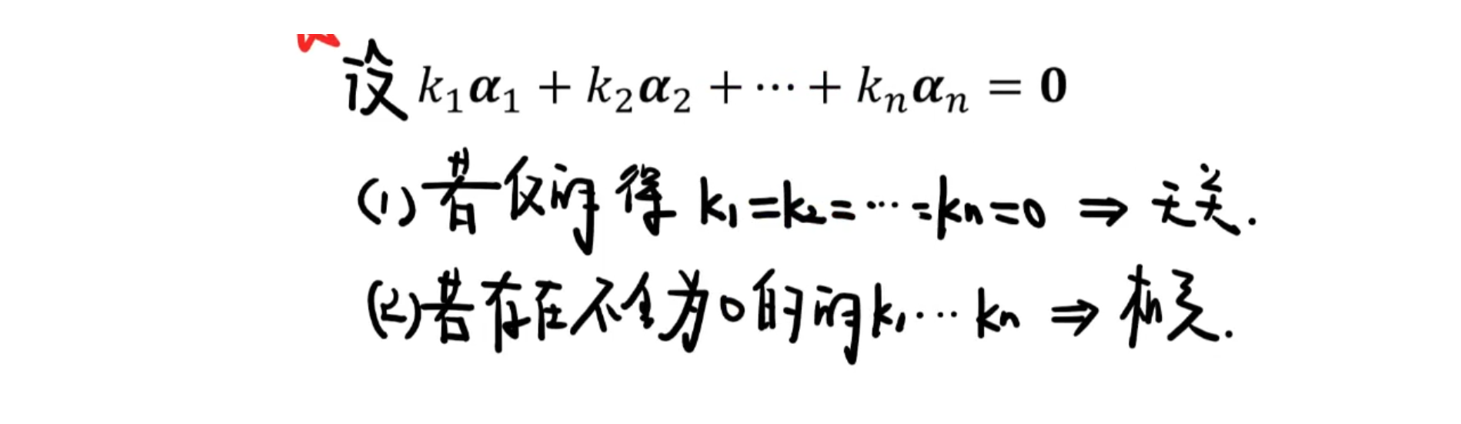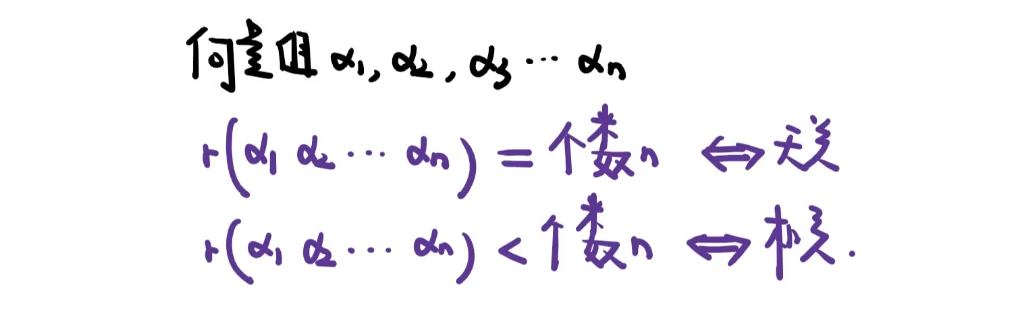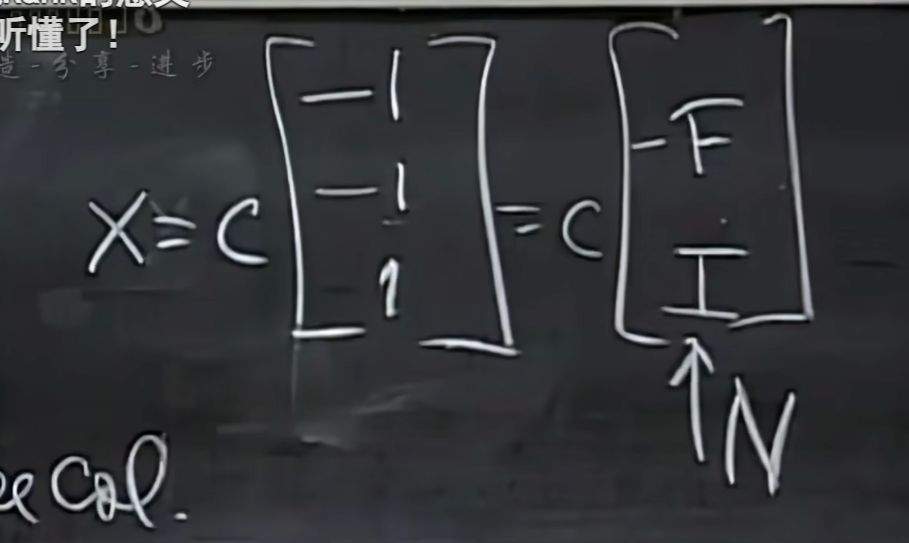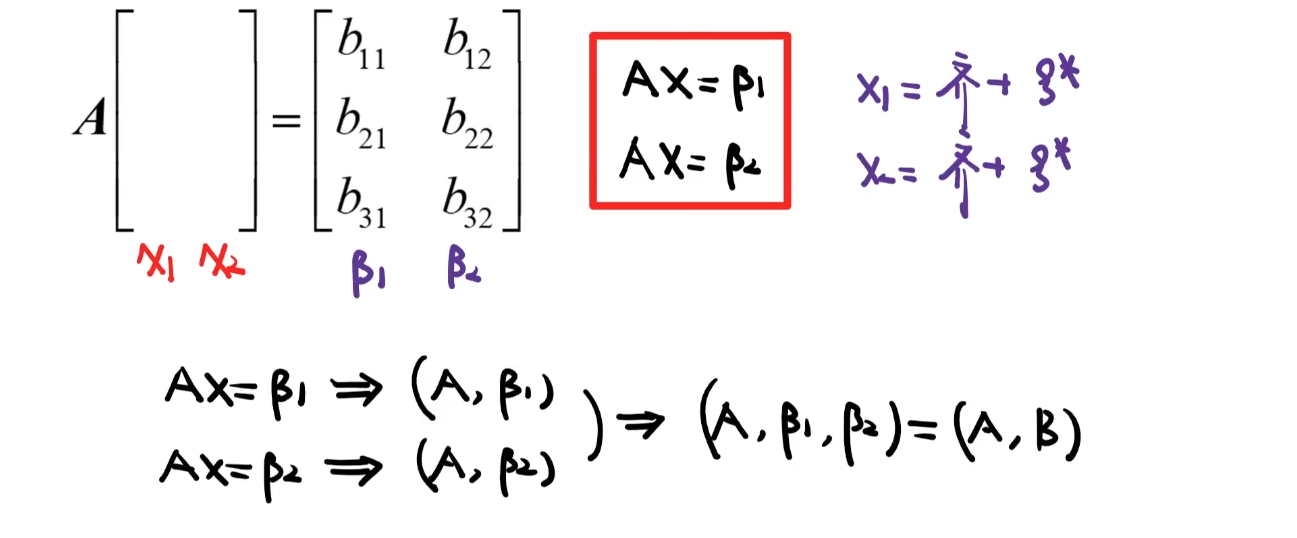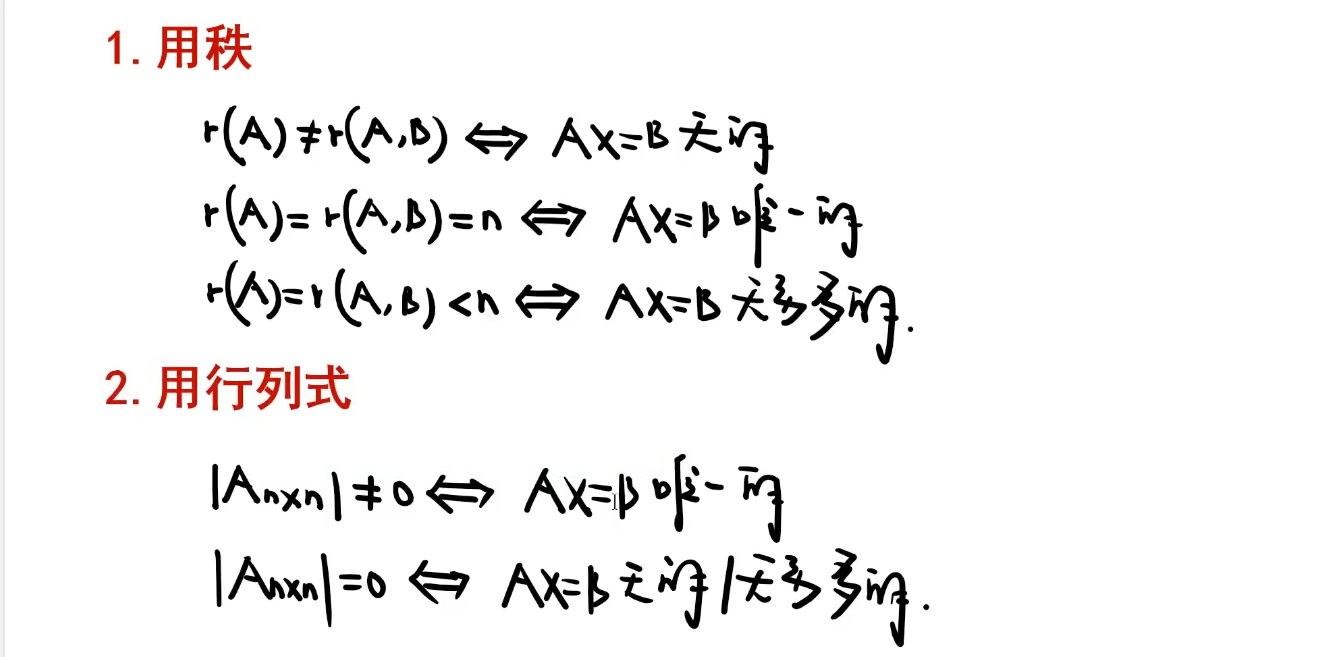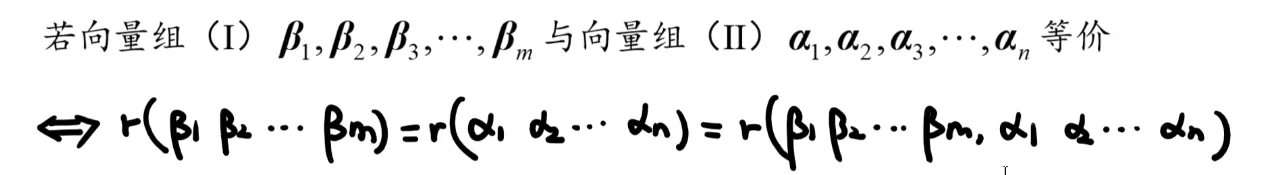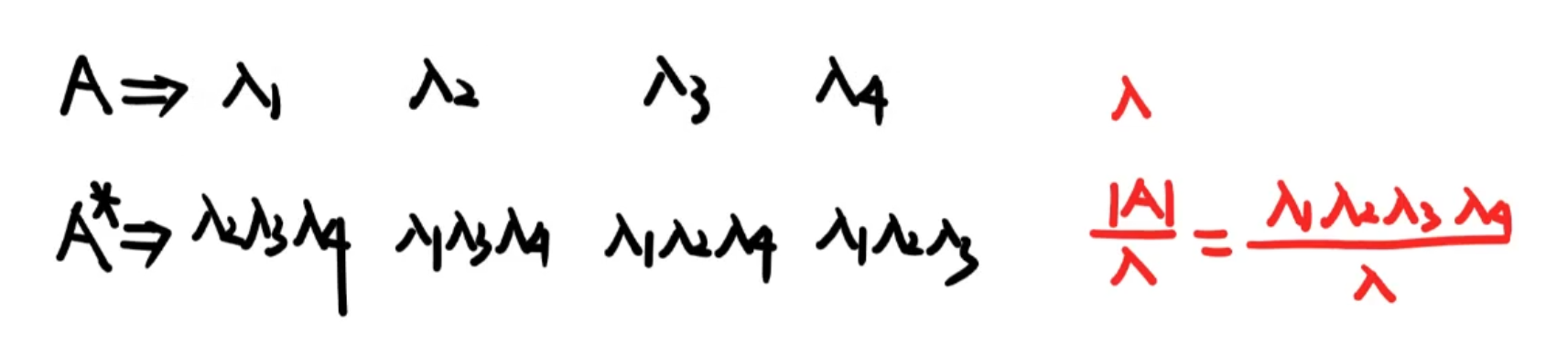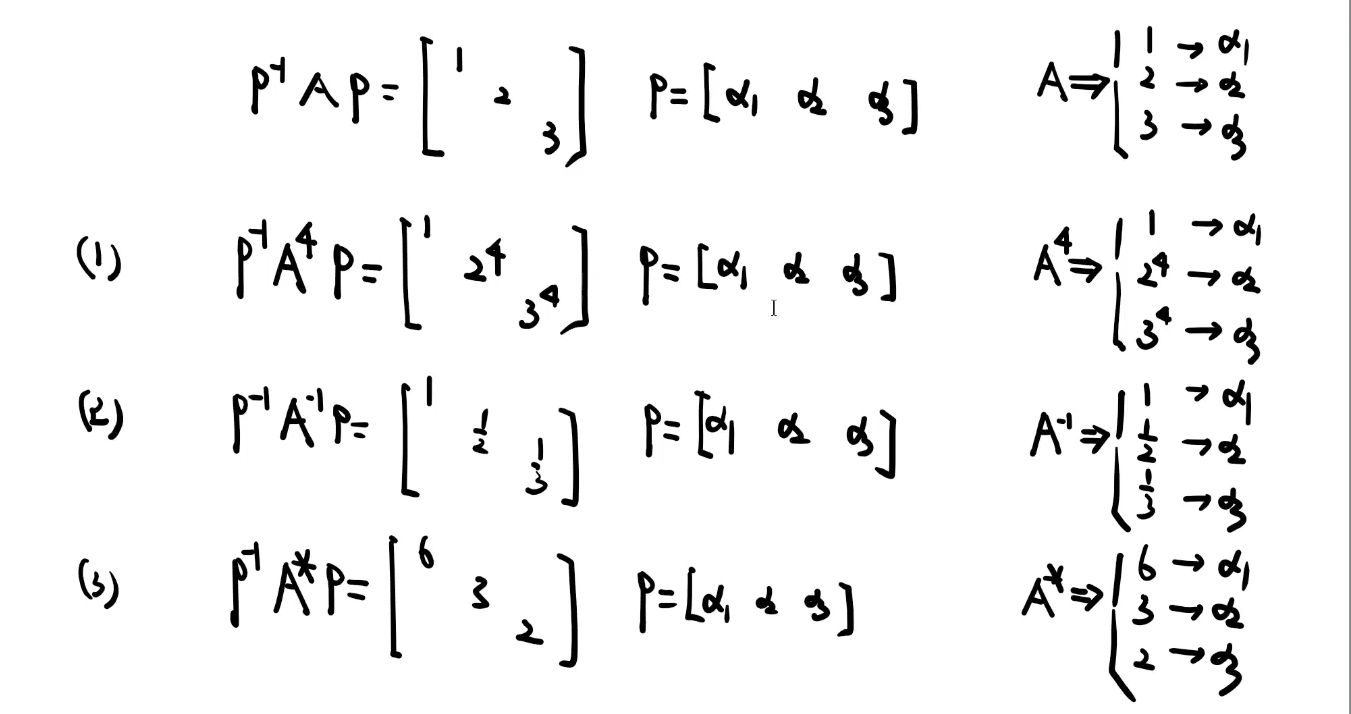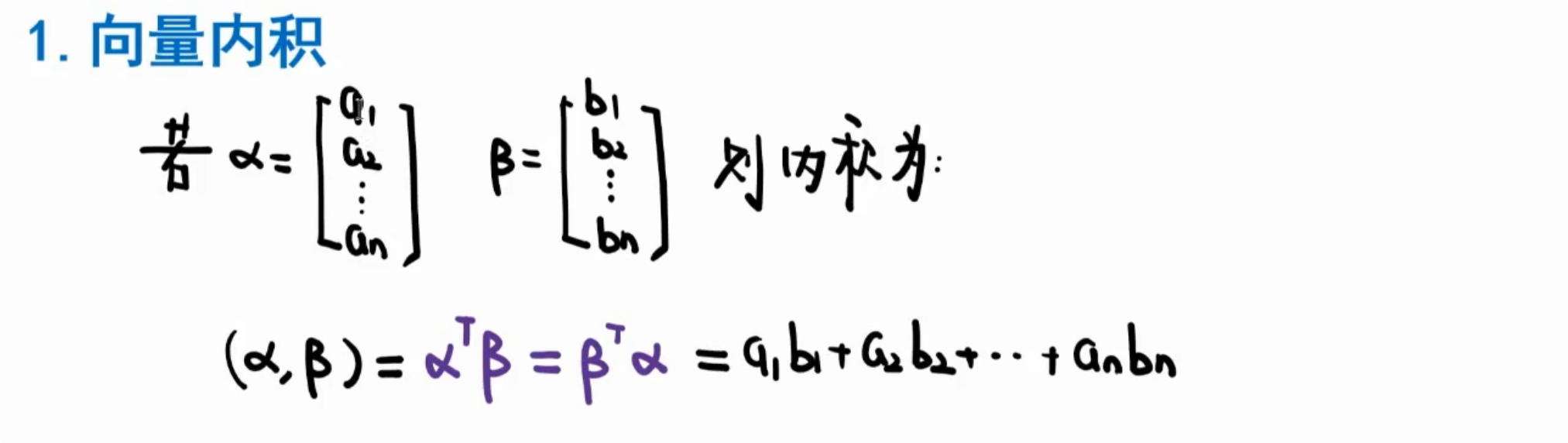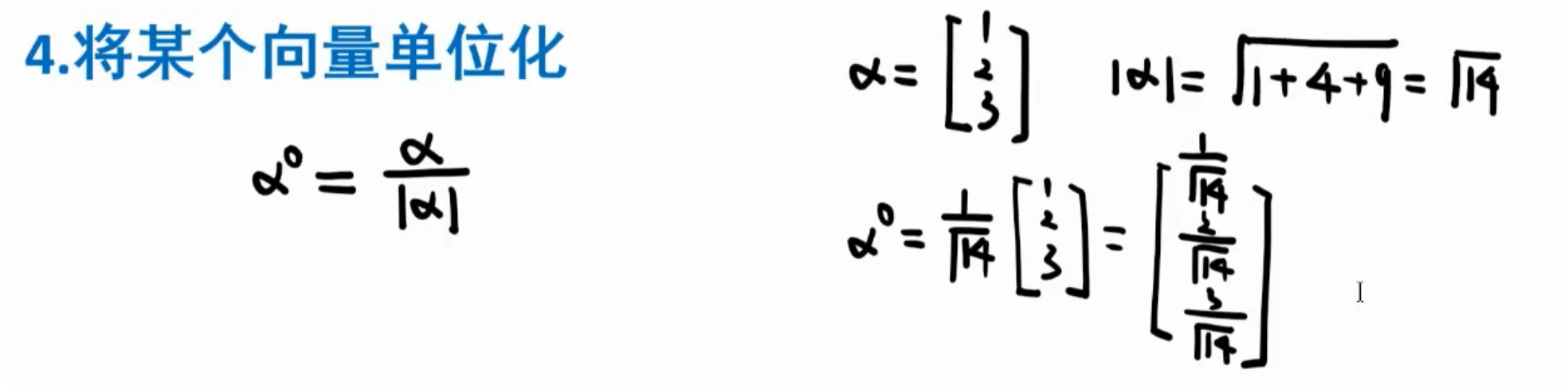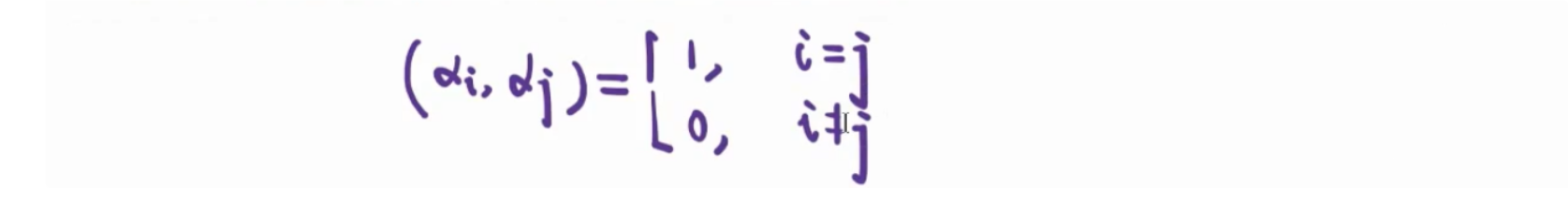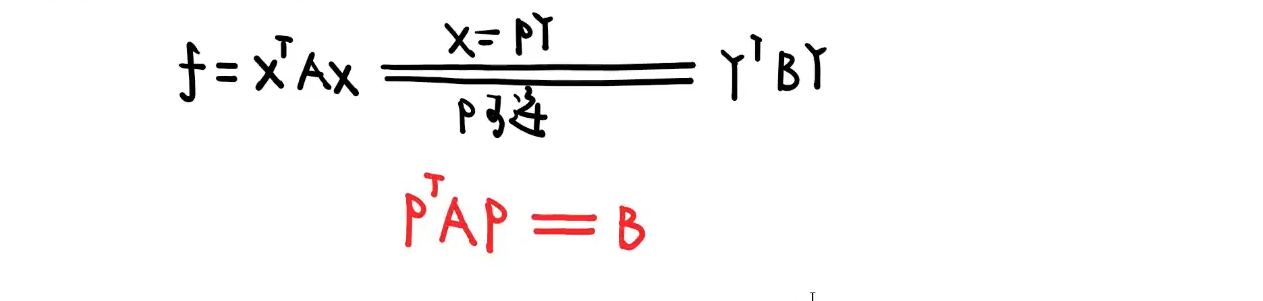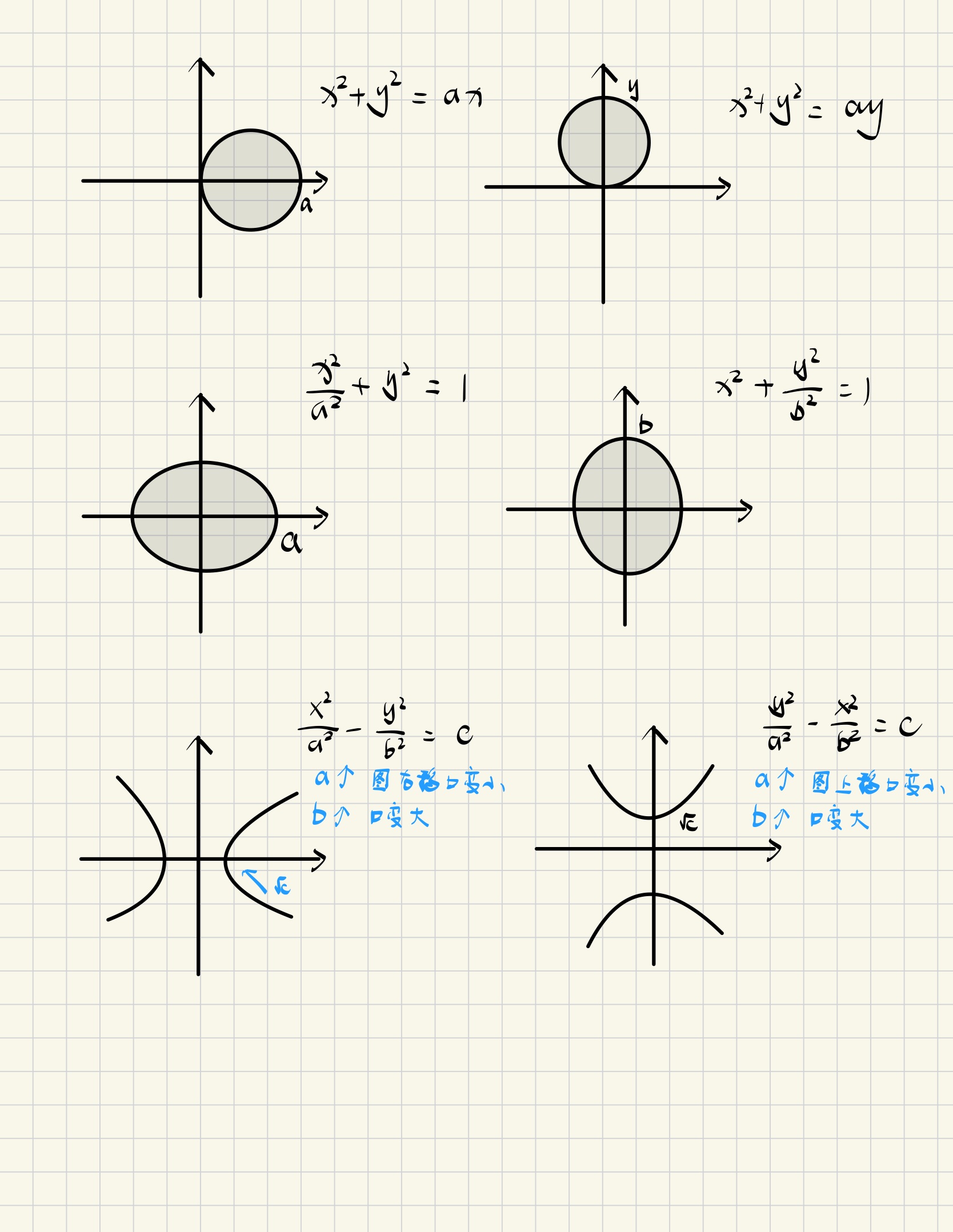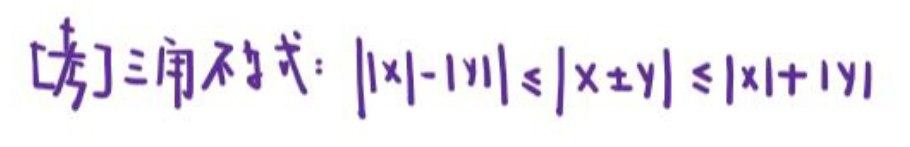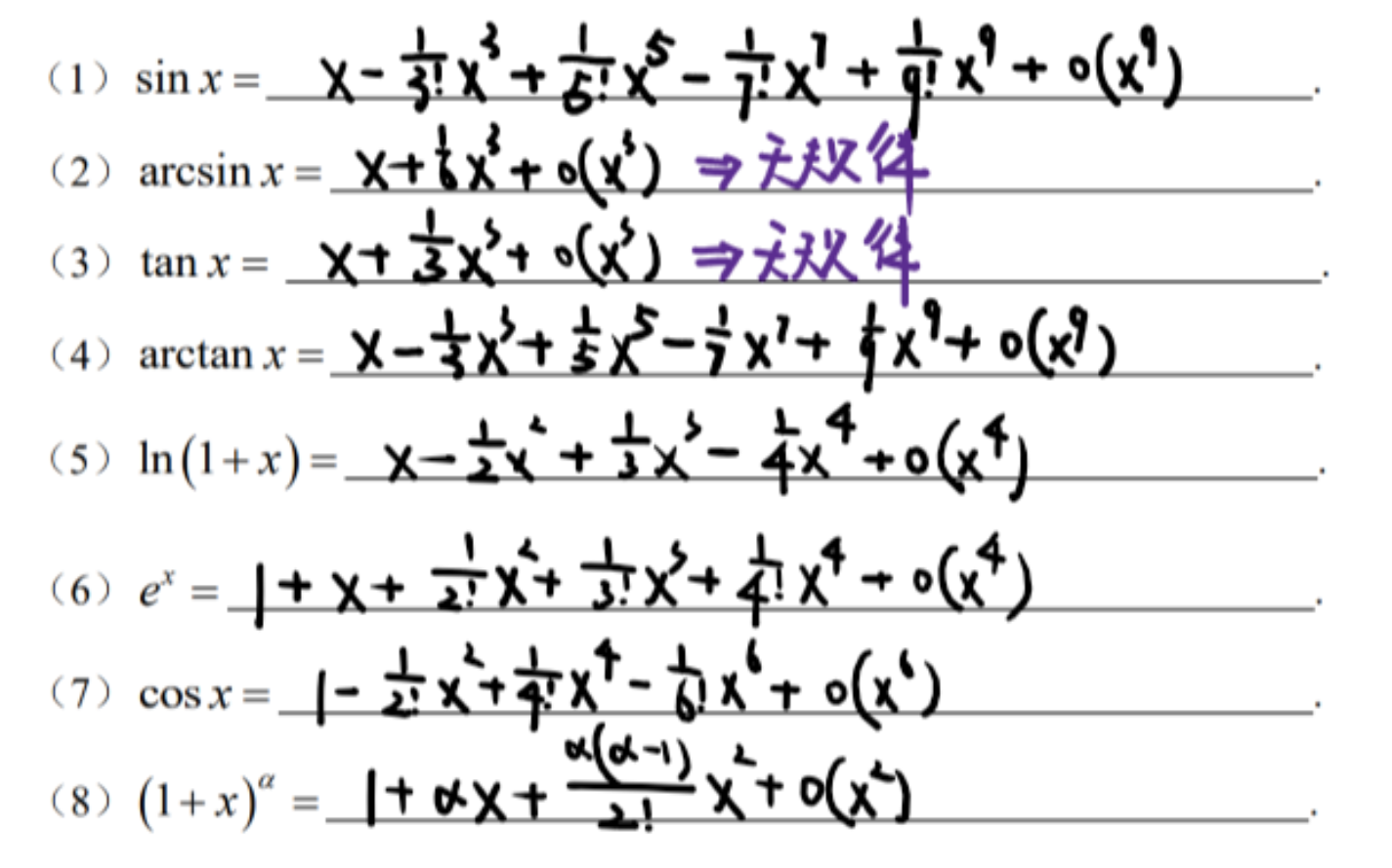考研高数笔记

一、极限

1️⃣极限定义及基本性质

①定义

• 无穷小：当$x$趋于$x_0$时，存在一个很小的数，$f(x)$和$f(x_0)$之间的差比这个数还要小。（差是绝对值） $lim_{x\to{x_o}}f(x)=A<=>{\forall}ε>0,{\exist}ξ>0，0<|x-x_o|<ξ时,|f(x)-A|<ε$
• 无穷大：当$x$趋于无穷大等于A时，存在一个很小的数，$f(x)$和A之间的差比这个数还要小。（差是绝对值）

②极限存在判定

充要条件

• 函数左右极限存在且相等➡️左右开弓法求极限

必要条件

• $f(x)$在$x=x_o$去心领域内有定义

③极限三大性质

唯一性

局部保号性

🎩Z摘帽保号性（两个尖号）

如果$f(x)$在$x_0$的极限大于0，那么在其去心领域内也大于0。

如果$f(x)$在$x_0$的极限≥0，那么无法推出任何结论（因为函数在0左右都有值）。

🎩D戴帽保号性（结论加等号）

如果在$x_0$的去心领域内$f(x)>0$，且极限存在等于A，那么$A≥0$。

如果在$x_0$的去心领域内$f(x)≥0$，且极限存在等于A，那么$A≥0$。

局部有界性

④有界定理

1. 初等函数在定义区间内均连续。
2. 初等函数有界区间的求解方法：找无定义点和选项端点，求左右极限，找连续区间✅

闭区间连续函数

闭区间内连续➡️开区间连续➕左端点右连续➕右端点左连续

开区间连续函数

左连续➕右极限存在➡️有界、右连续➕左极限存在➡️有界

2️⃣无穷小量及无穷大量

①定义

1. $0*有界=0$
2. $无穷大*有界≠无穷大$（可能振荡）

②无穷小阶

• 高比低是0，低比高是无穷

• 和取低阶原则（若f(x)为m阶无穷小，g(x)为n阶无穷小，fg=m+n阶无穷小，f±g不为min(f,g)，也就是不满足和取低阶，因为两个同阶的可能碰撞出更大的火花，所以前提要不同阶）

• 乘法叠加原则

  $o(x^2)o(x^3)=o(x^5)、o(x^2)x^2=o(x^4)、\frac{o(x^2)}{x}=o(x)、\frac{o(x^3)}{o(^x)}≠o(x^2)$【⚠️Attention！】

• 数乘无关

  $k*o(x^2)=o(kx^2)=o(x^2)$

• 二者比阶：

二者之比	类型
1	等价无穷小
A	同阶非等价无穷小
∞	低阶
0	高阶

3️⃣泰勒公式

泰勒公式将函数变成多项式处理

①泰勒定理

麦克劳林公式

x0等于0的泰勒公式

• $f(x)-g(x)$：展开到相消不为0
• $\frac{f(x)}{g(x)}$：展开到同阶

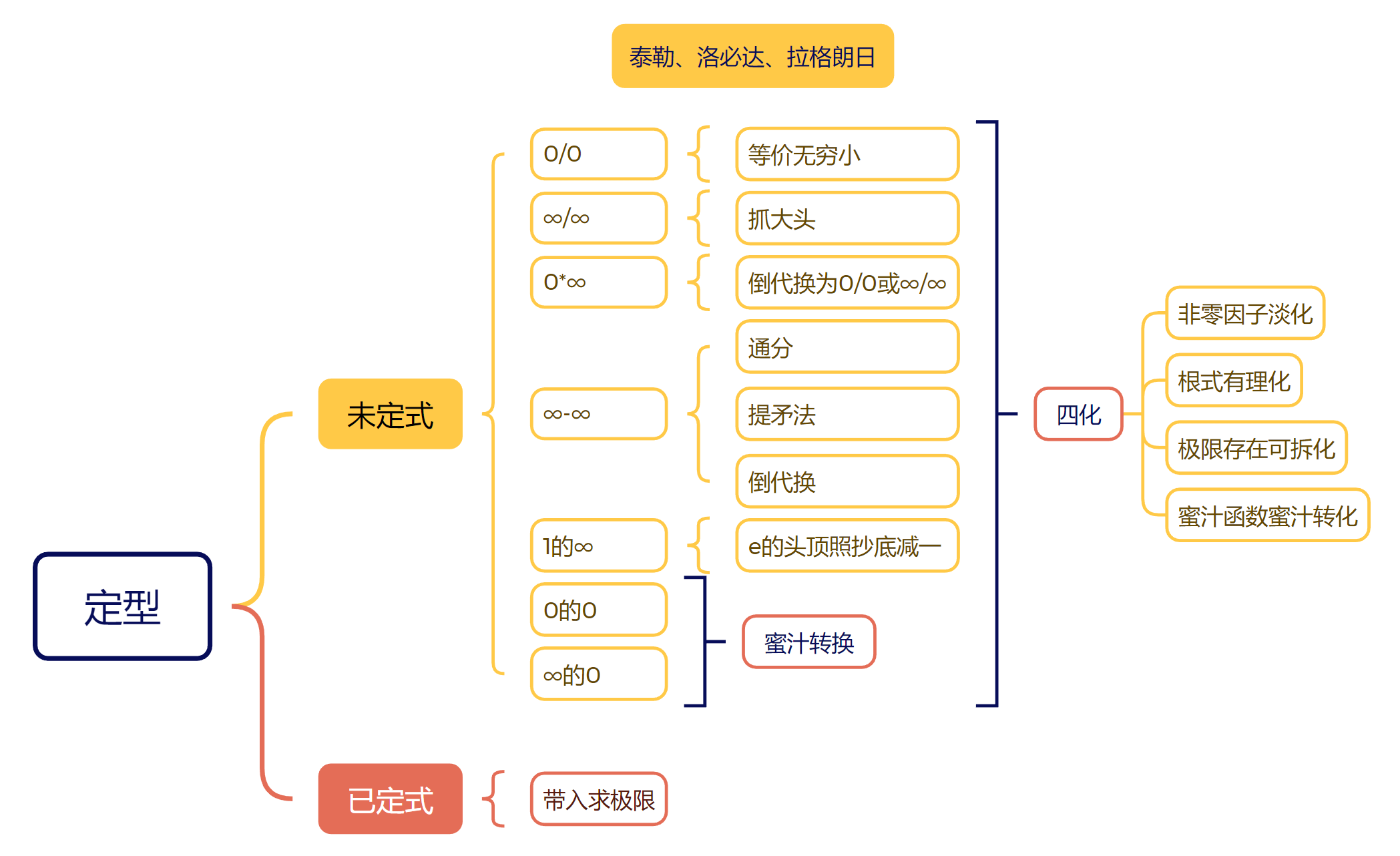
4️⃣极限计算

①函数极限

先定形后定法，定法之前先四化

计算方法	条件	注意
洛必达法则	$\frac{0}{0}或\frac{∞}{∞}$、分子分母极限存在、结果是A或∞	1、洛必达法则能否成立是由求导后的极限决定 2、洛必达法则不能前推后，如果后面震荡了就与前面的无关了
四则运算	极限存在	加减乘除都可拆，前提是存在，除的时候分母不为0
补项法	无	例如同时加减x凑常见等价无穷小
非零因子先算	遇到乘除法非零因子可以先计算出来	只有乘除，加减法不能用
拉格朗日中值定理	相同对应法则两函数做差	写“ξ介于两个之间”
泰勒展开	无	展开到相消不为0或同阶项
等价无穷小	趋于0时可用

极限四则运算性质

第一项	运算符	第二项	结果
存在	加减	存在	存在
存在	加减	不存在	不存在
不存在	加减	不存在	未知
存在	乘	存在	存在
存在	乘	不存在	未知
不存在	乘	不存在	未知

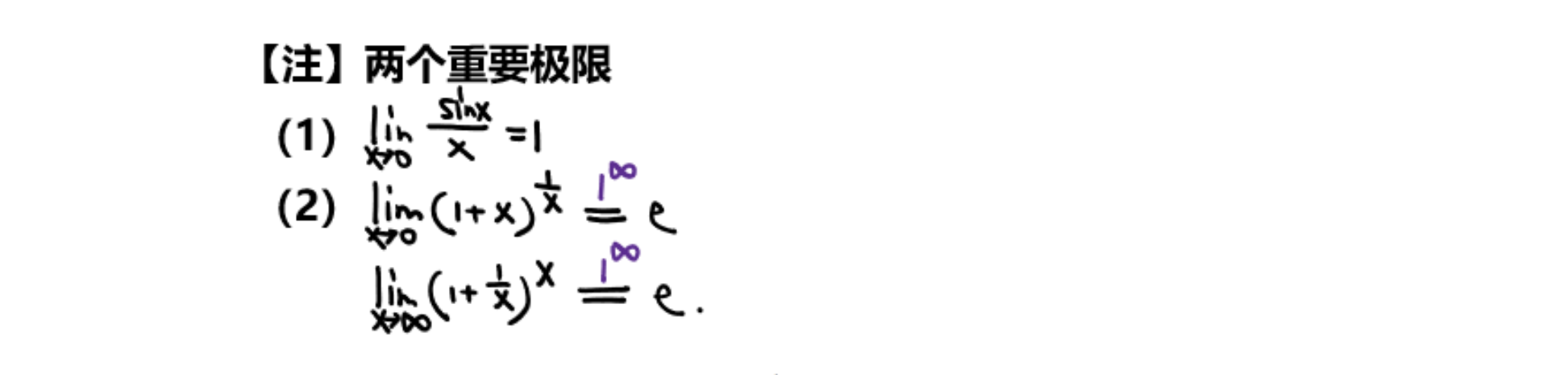
重要极限

两个重要极限

0*∞重要极限

∞的0易错点

考法

左右开弓法求极限

极限形式	左极限	右极限
$e^∞$	$+∞$	0
$arctan∞$	π/2	-π/2
$x{\to}0,	x	$
分段函数分段点处
取整函数$x{\to}a,[x]$
$x{\to}0,1/x$	+∞	-∞

求极限中待定参数

定型后是未定式，那就按照未定式来处理。定型后不是未定式，不，它一定是未定式，因为结果是一个数字一定是未定式。

已知极限求另外一个极限

• 凑另一个极限

• 极限反解定理（万能）

  $\lim_{x\to0}f\left(x\right)=a\Leftrightarrow f\left(x\right)=a+\alpha ，\alpha为高阶无穷小$

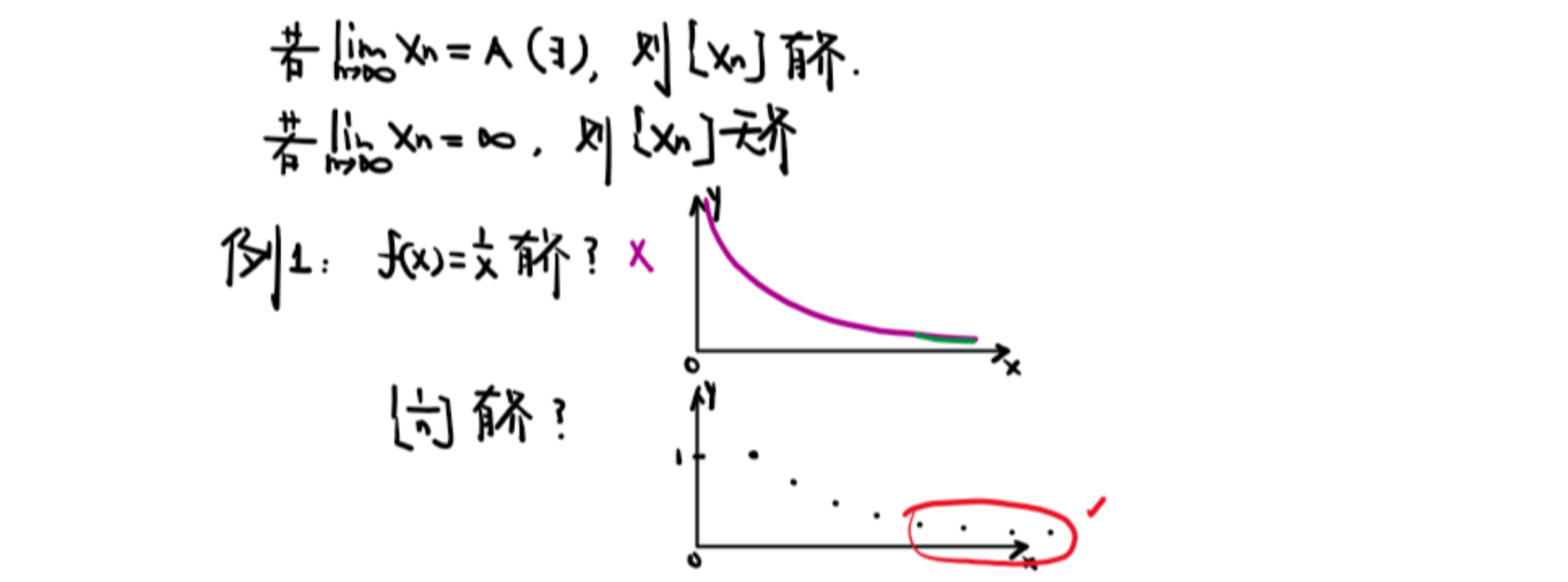
②数列极限

定义

数列极限只有一种趋向，那就是正无穷，在大于某个数后，所有的点都趋于A。

子数列

例如$[X_n]$的子数列$[X_{2n}]$、$[X_{3n}]$。

数列极限的性质

唯一性

保号性

有界性

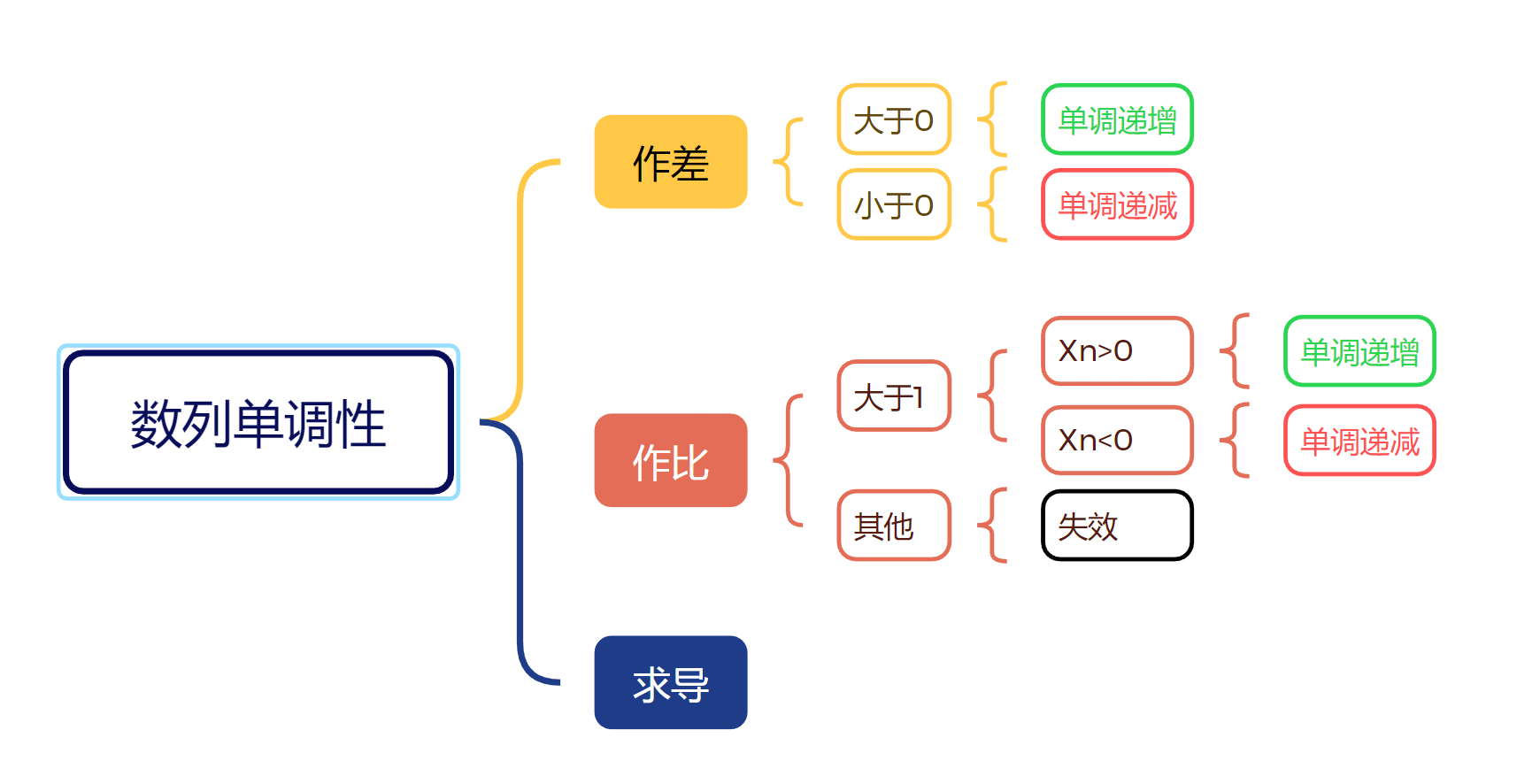
数列极限计算

• 数列极限只有一种趋向——无穷大
• 数列极限不可以使用洛必达，需要先连续化处理
• $lim_{n\to∞}\sqrt[n]{a}=1(a>0)$
• $lim_{n\to∞}\sqrt[n]{n}=1(a>0)$②

夹逼定理

• n项和问题：放缩分母使其可以相加
• 开n次方问题：都变成最大值，使用②式

单调有界必有极限

递推公式题型

1. 证明有界性

   

   小技巧、基本不等式（见附录）

2. 证明单调性

   

3. 求极限（可以先求极限进而确定有界性）

不定积分

有理分式

真分式

• 分子凑分母的导数

  

• 因式分解

  

假分式

眼瞅分母写分子，将其变成真分式，然后再使用真分式的求解方法。

无理根式

根号换元

直接令t等于一坨，反解出x，dx计算出来丢前面。

三角换元

• $1+tanx=secx^2$
• $sinx+cosx=1$

三角函数

见到双眼要发光系列✨

\[1{\pm}sinx=(sin\frac{x}{2}{\pm}cos\frac{x}{2})^2\] \[1+cosx=2cos^2\frac{x}{2}\] \[1-cosx=2sin^2\frac{x}{2}\]

万能公式

\[\frac{A}{Bsinx+Ccosx+D}\]

---

分析：分子为常数，分母为sinx和cosx的倍数组合，将$tan\frac{x}{2}$设为t后，x就等于$2arctant$，因此dx就等于$\frac{2}{1+t^2}dt$，将其放到d前面后分母上正好可以化简抵消。

M分母+N分母导数

\[\frac{Asinx+Bcosx}{Csinx+Dcosx}\]

---

分析：分子分母为sinx和cosx的倍数组合，可以将其整理成$\frac{M(Asinx+Bcosx)+N(Asinx+Bcosx)^{‘}}{Asinx+Bcosx}$，前半部分化简为一个常数，后半部分进行凑微分。 写出方程，对于sinx和cosx的系数列出两个=方程，解出M和N。

积化和差

\[sin(Ax)sin(Bx)\] \[cos(Ax)cos(Bx)\] \[sin(Ax)cos(Bx)\]

使用积化和差公式整理后很好积分。

定积分

定积分性质

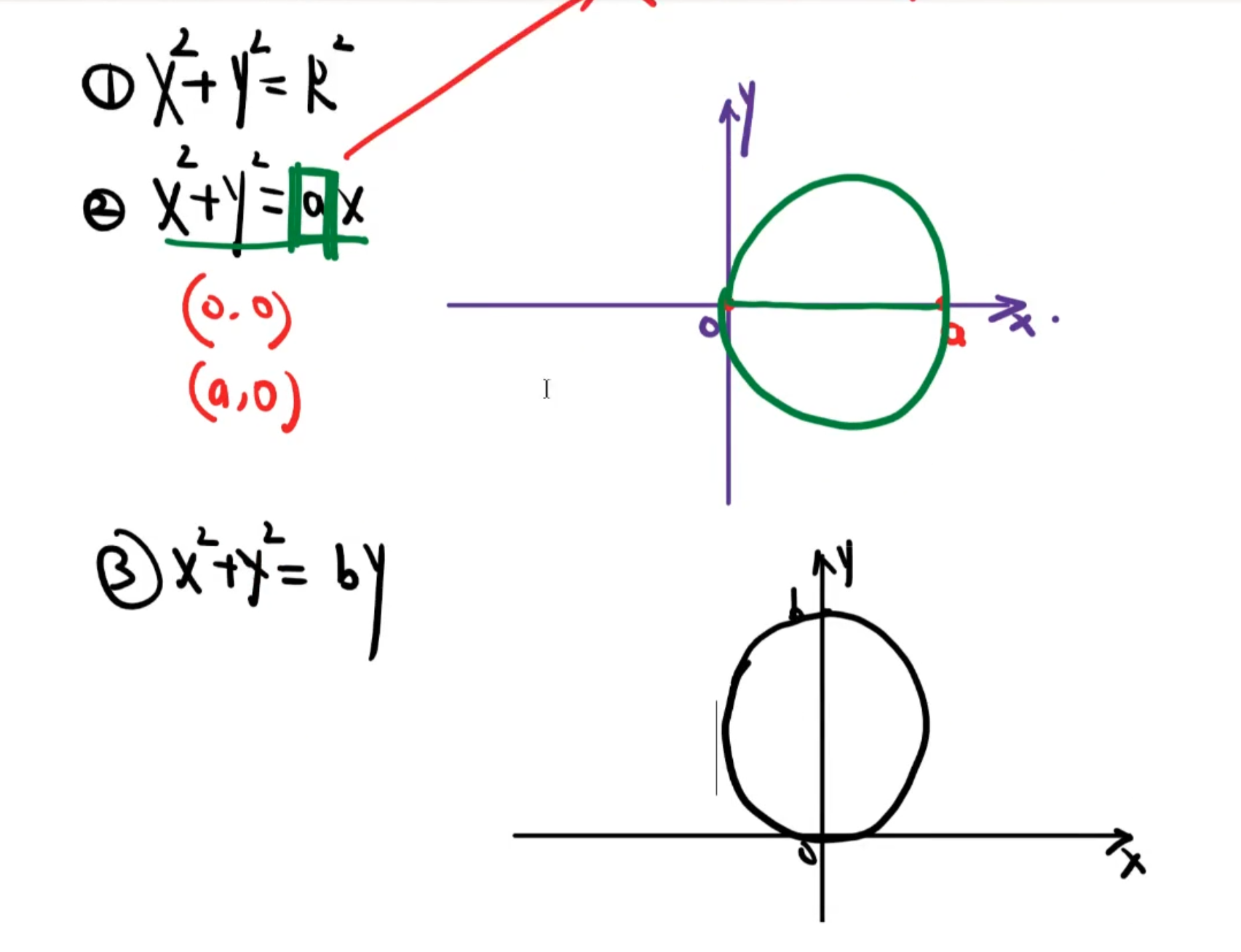
定积分几何意义

圆面积

偏心圆

椭圆

定积分存在定理

充分条件

• f(x)在[a,b]连续

• f(x)在[a,b]有界，且有有限个第一类间断点

必要条件

• f(x)在[a,b]有界

定积分的计算

直接计算

凑微分

分部积分

第二类换元法

技巧计算

几何意义

奇偶性

周期性

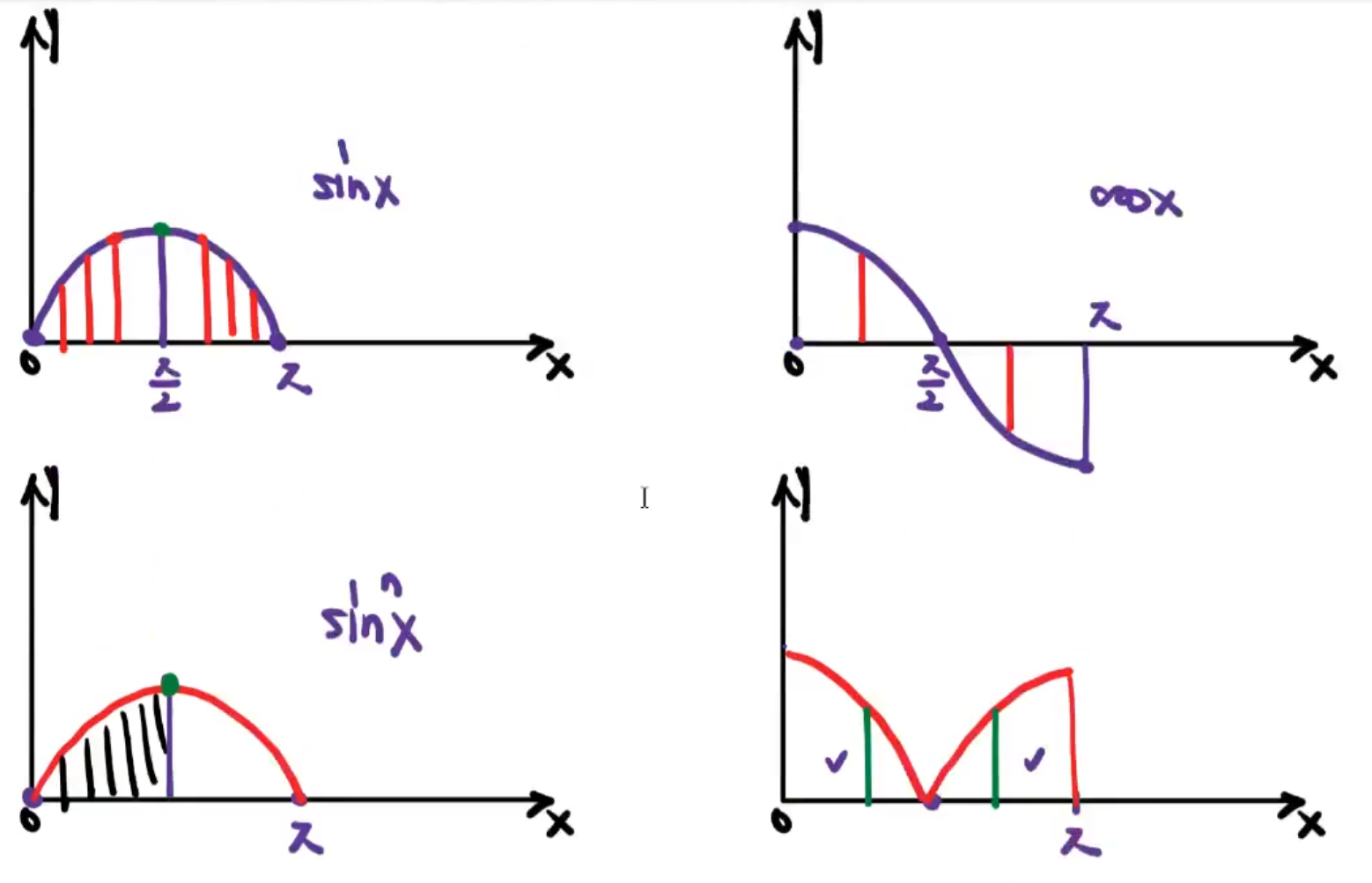
区间再现公式

点火公式一家人

重要结论

根据区间再现公式推出的重要结论： \(\int_0^\frac{\pi}{2}f(sinx)dx=\int_0^\frac{\pi}{2}f(cosx)dx\)

\[\int_0^{\pi}xf(sinx)dx=\frac{\pi}{2}\int_0^{\pi}f(sinx)dx\] \[\int_{-a}^{a}f(x)dx=\int_{0}^{a}[f(x)+f(-x)]dx\]

题型

对称区间定积分

1. 奇偶性
2. 公式
3. 一半区间打开，一半进行负代换

定积分的应用

几何应用

平面面积

直角坐标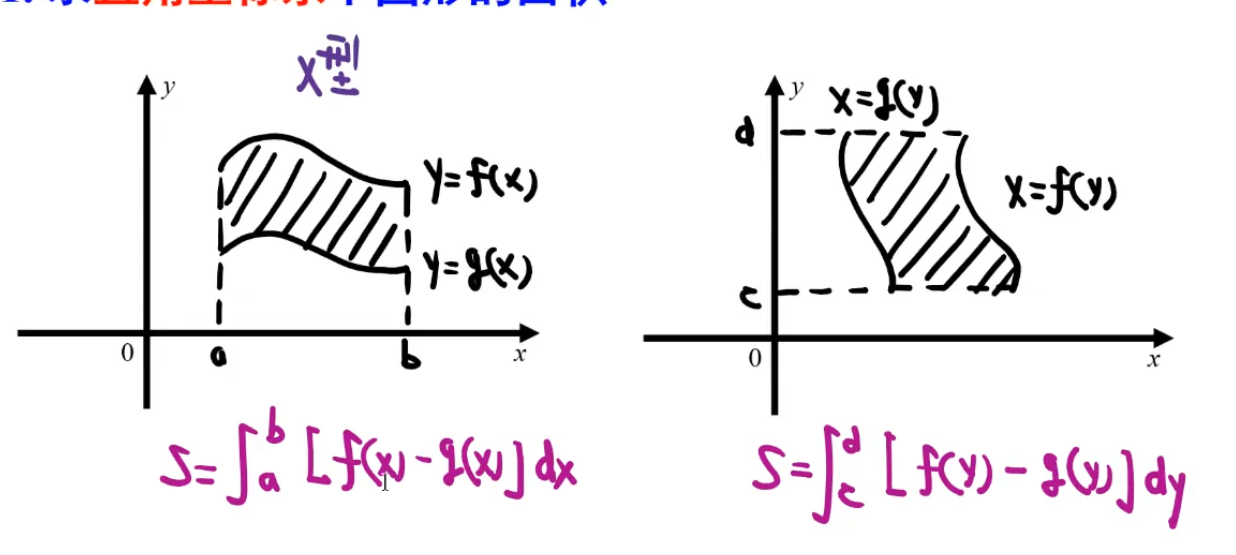

\[S=\int_a^{b}f(x)dx\]

或者 \(S=\int_a^{b}f(y)dy\)

高减低，右减左，确保面积为正。

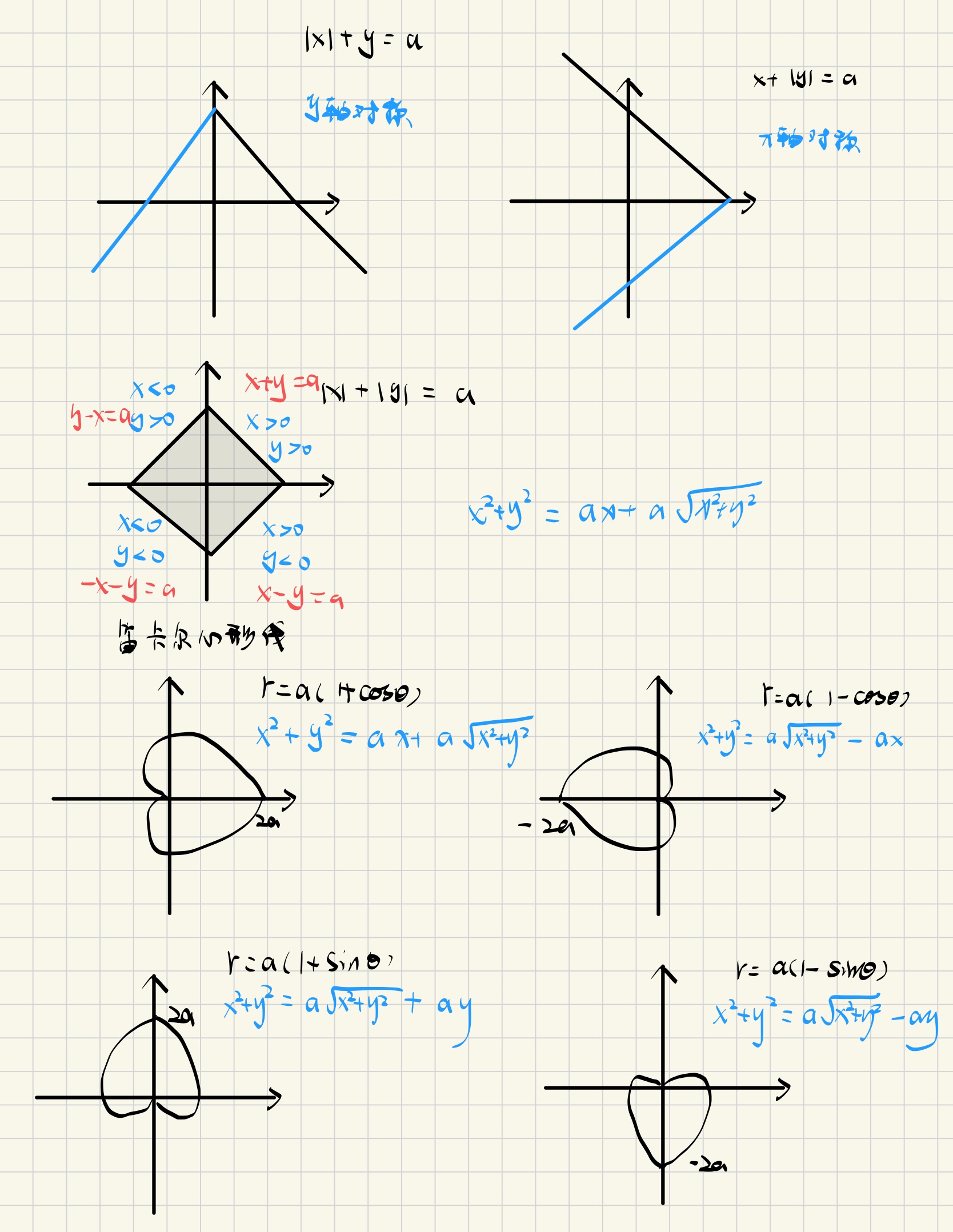
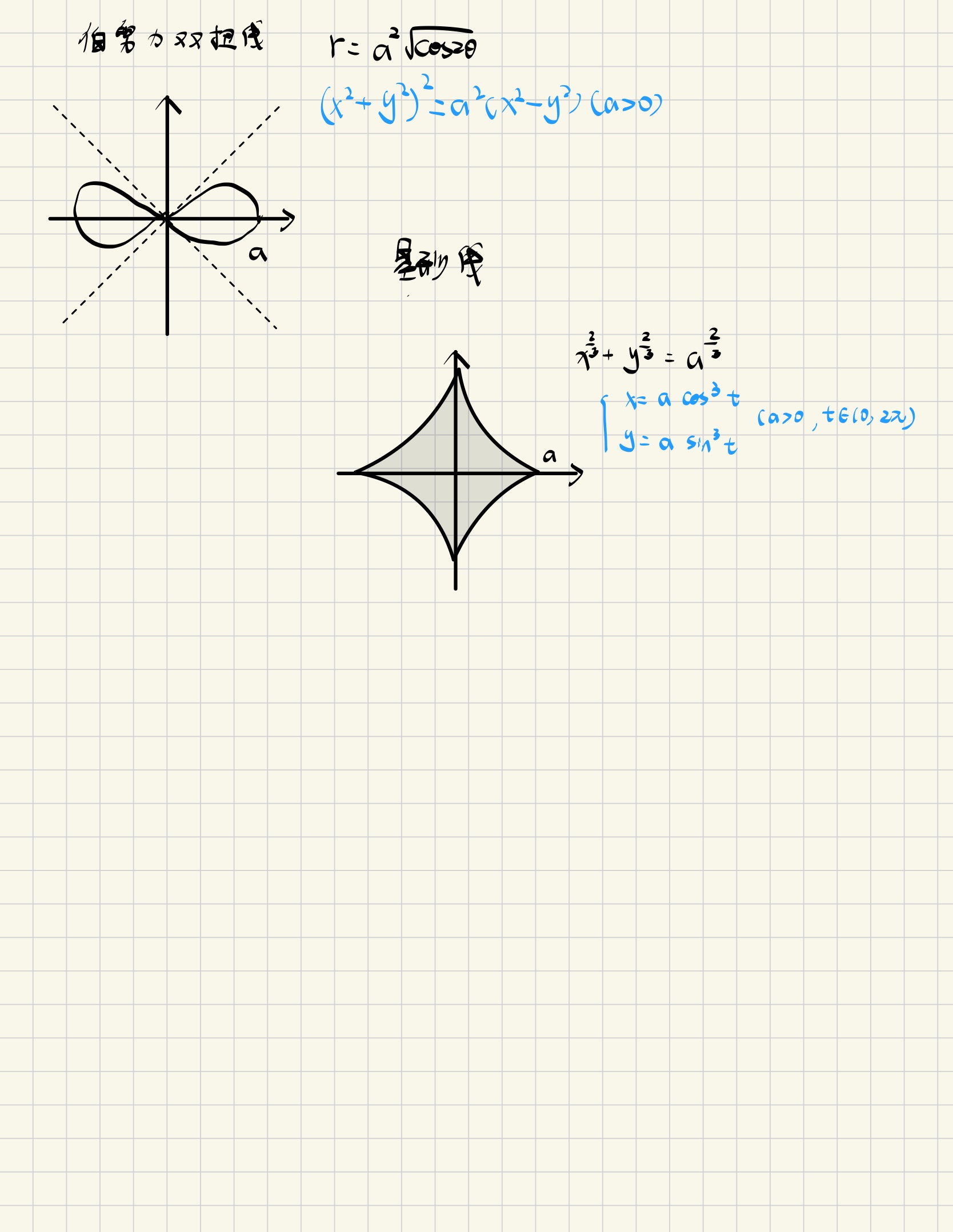
极坐标系

\[S=\frac{1}{2}\int_{\alpha}^{\beta}r^2(\theta)d\theta\]

补充：扇形面积公式

\[S=\frac{1}{2}LR=\frac{1}{2}{\theta}R^2，其中弧长L={\theta}R\]

补充：重要的极坐标曲线（见附录1）

参数方程

\[S=\int_{a}^{b}y_(t)x^{'}_{(t)}dt\]

旋转体体积

直角坐标

• 绕x轴

\[V_x=\int_a^b{\pi}y^2dx=>其中{\pi}y^2为圆柱体的表面积,dx为圆柱体的高\]

• 绕y轴

\[V_y=\int_a^b2{\pi}xydx=>其中2{\pi}x为周长即展开长方体的长,y为长方体的高,dx为长方体的厚度\]

极坐标系

使用极坐标方程将直角坐标系下的公式中x、y、dx代换掉。

参数方程

使用参数方程将直角坐标系下的公式中x、y、dx代换掉。

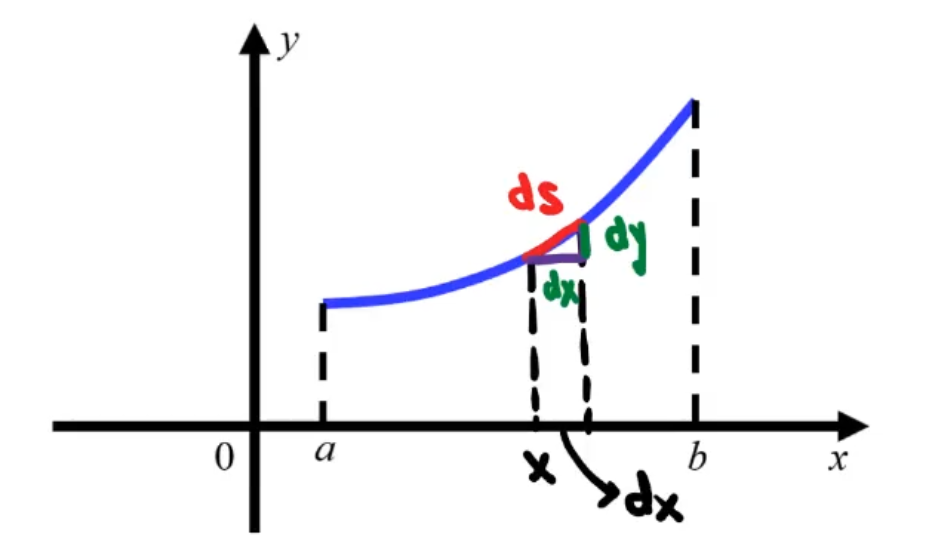
弧长L

积分限从小写到大（牵扯到弧微分一律从小写到大）

易得： \(ds=\sqrt{(dx)^2+(dy)^2}\)

直角坐标

\[L=\int_a^b\sqrt{1+(y^{'}_{x})^2}dx\]

参数方程

\[L=\int_\alpha^\beta\sqrt{(x^{'}_t)^2+(y^{'}_t)^2}dt\]

极坐标

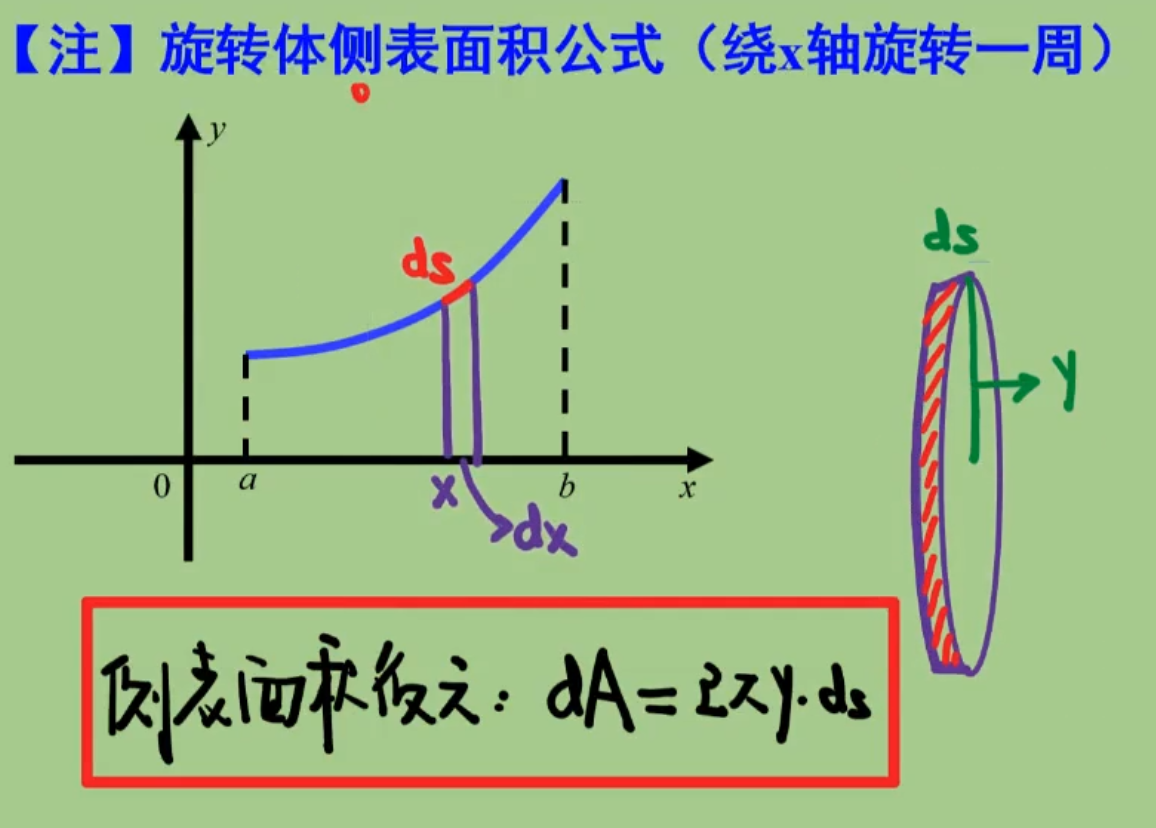
\[L=\int_\alpha^\beta\sqrt{r^2+(r^{'}_\theta)^2}d\theta\]

旋转侧表面积

积分限从小写到大（牵扯到弧微分一律从小写到大）

直角坐标

公式中的y是高，要确保是正的

\[S=\int_a^{b}2\pi{y}\sqrt{1+(y^{'}_{x})^2}dx=>其中a≤x≤b\]

参数方程

\[S=\int_\alpha^{\beta}2\pi{y_{t}}\sqrt{(x^{'}_t)^2+(y^{'}_t)^2}dt=>其中\alpha≤x≤\beta\]

极坐标

\[S=\int_\alpha^{\beta}2{\pi}r*sin(\theta)\sqrt{r^2+(r^{'}_\theta)^2}d\theta=>其中\alpha≤x≤\beta\]

物理应用

变力做工问题

使用微元法。

力的问题

变限函数

变限函数存在性

变现函数存在性跟着定积分存在定理一样。

变限函数求导（标准型）

使用条件：被积分函数连续

\[\Phi'(x)=\frac{d}{dx}\int_{\phi(x)}^{\varphi(x)}f(t)dt=f[\varphi(x)]\varphi'(x)-f[\phi(x)]\phi'(x)\]

上限移进去上限求导减下限移进去下限求导

证明：

变限函数求导（非标准型）

• 将自变量踢出去，用乘法求导法则求导
• 换元

牛逼爸

反常积分

反常积分判断

• 积分区间无穷

• 存在瑕点

  1. 找无定义点
  2. 判断无定义点是否为无穷间断点

反常积分计算

四则运算

重要反常积分

1️⃣区间大的影响，大的喜欢大的，大于1就收敛。

2️⃣区间小的影响，小的喜欢小的，小于1就收敛。

3️⃣等于1永远收敛。

反常积分奇偶性

比较审敛法

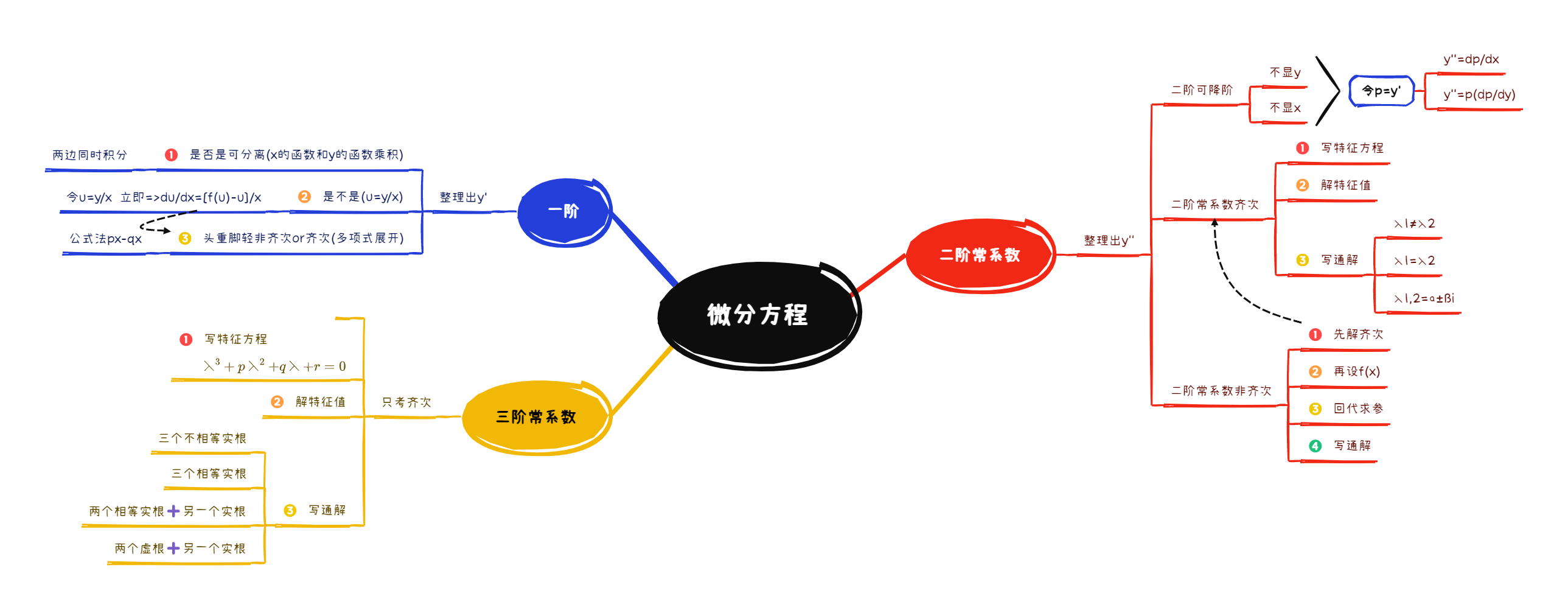
常微分方程

一阶

可分离变量

y的导数可以写成f(x)和g(y)组合的形式。

解法： \(\frac{1}{g(y)}dy=f(x)dx\)

\[=>\int\frac{1}{g(y)}dy=\int{f(x)}dx\]

注意事项

1. 通解≠全部的解，除数为0的时候不用管
2. 整理的时候出现ln常数加lnc
3. 出现ln积分绝对值要加
4. 边界条件带入得到这个情况下的特解

一阶齐次

通解结构

\[y=C*齐次解\]

一阶非齐次

高阶

二阶可降阶

二阶齐次线性

形式

通解结构

二阶非齐次线性

形式

通解结构

二阶常系数齐次

考研只考察这种类型的求解

线性微分方程的反问题

要想求方程必先知通解 要求非齐次必先求齐次

反求特征值

三种形式判断出类型。

二阶常系数非齐次

线性微分方程的叠加定理

三阶常系数齐次线性方程

中值定理

1️⃣有界定理

2️⃣最值定理

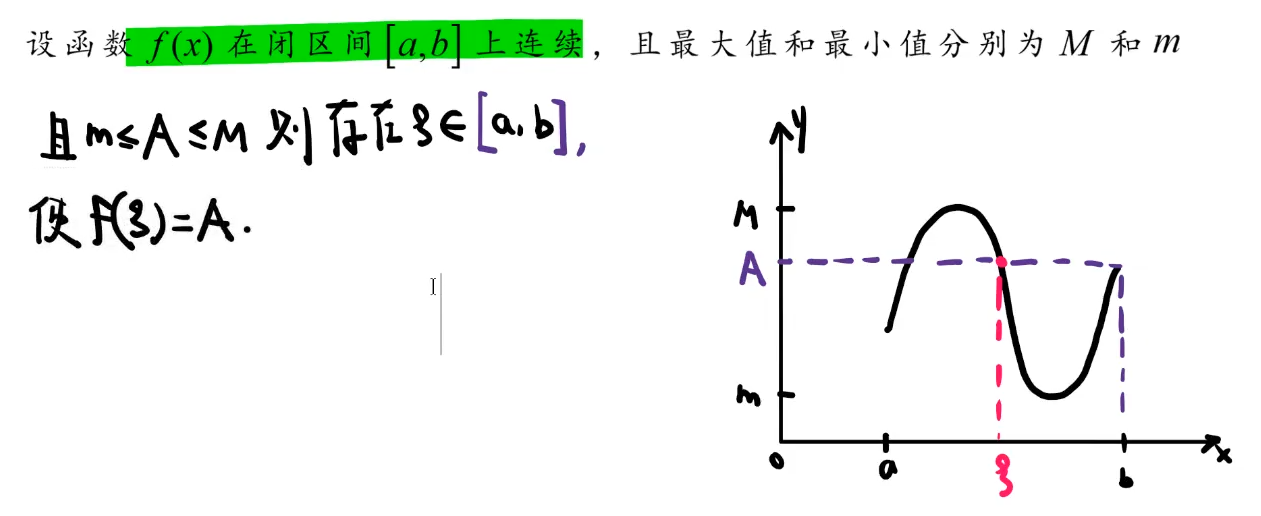
3️⃣介值定理

结论下的一定是闭区间！！！

4️⃣零点定理

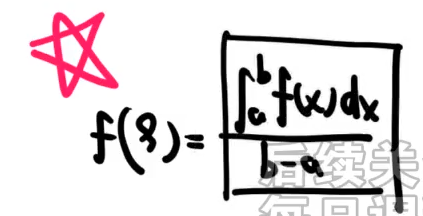
5️⃣积分中值定理

证明：最值定理=>比较定理=>介值定理

积分平均数

6️⃣费马定理

取极值且可导即导数为0

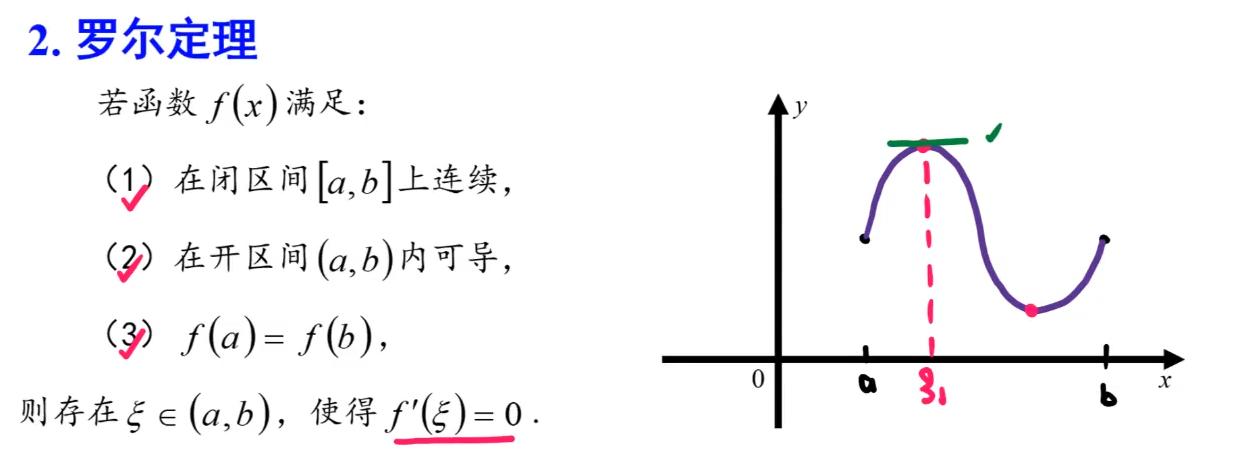
7️⃣罗尔定理

使用场景：证明一个中值点，一个等式等于0

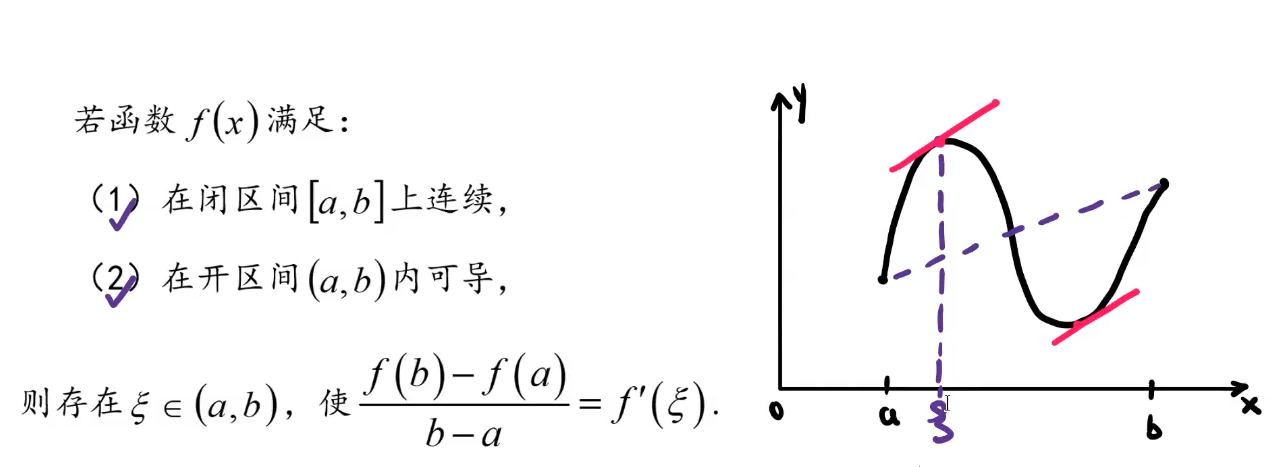
8️⃣拉格朗日中值定理

9️⃣柯西中值定理

🔟泰勒定理

求某一点的n阶导数值

定理	皮亚诺余项	拉格朗日余项
条件	在某一点处n阶可导	在点领域成立
结论	在区间内n+1阶可导	在区间内成立

多元函数微分学

1️⃣基本概念

多元函数的因、中间、自变量

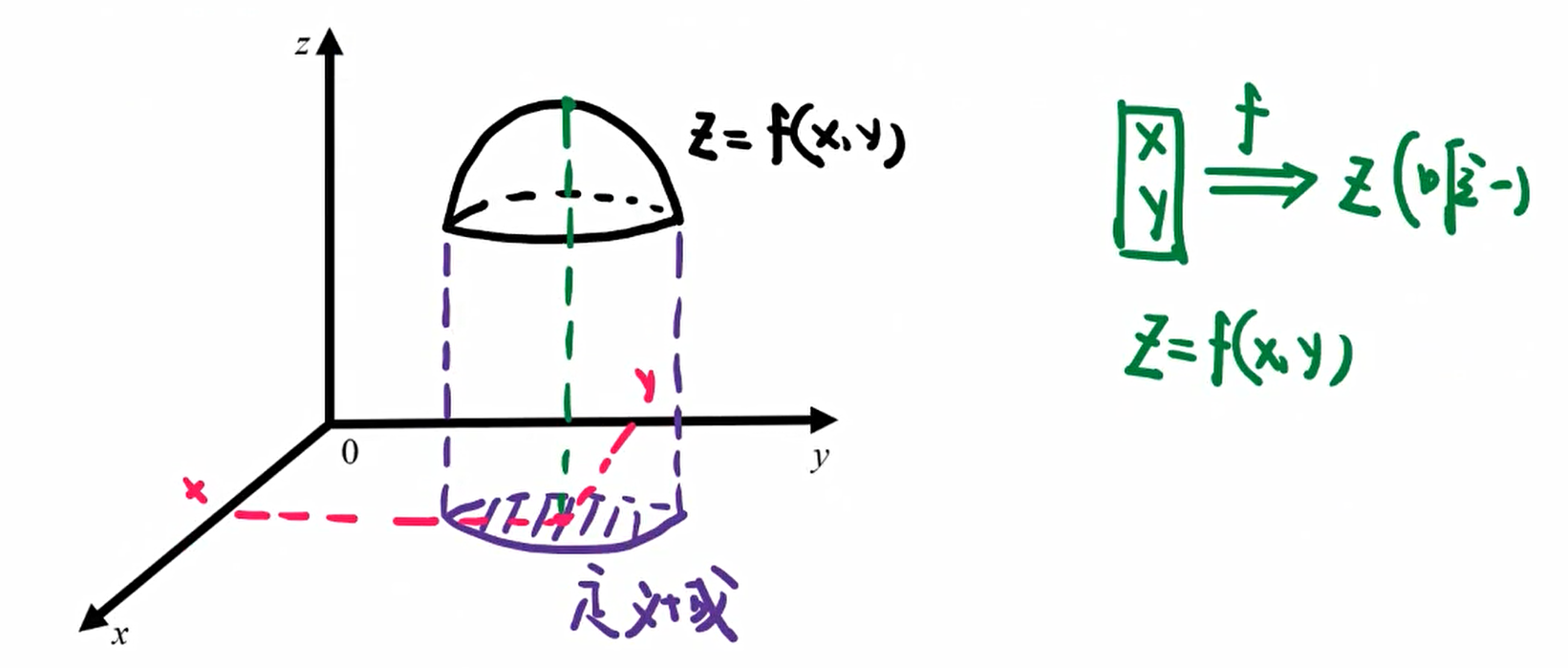
①二元函数几何意义

二元函数就是三维空间下的一个曲面。

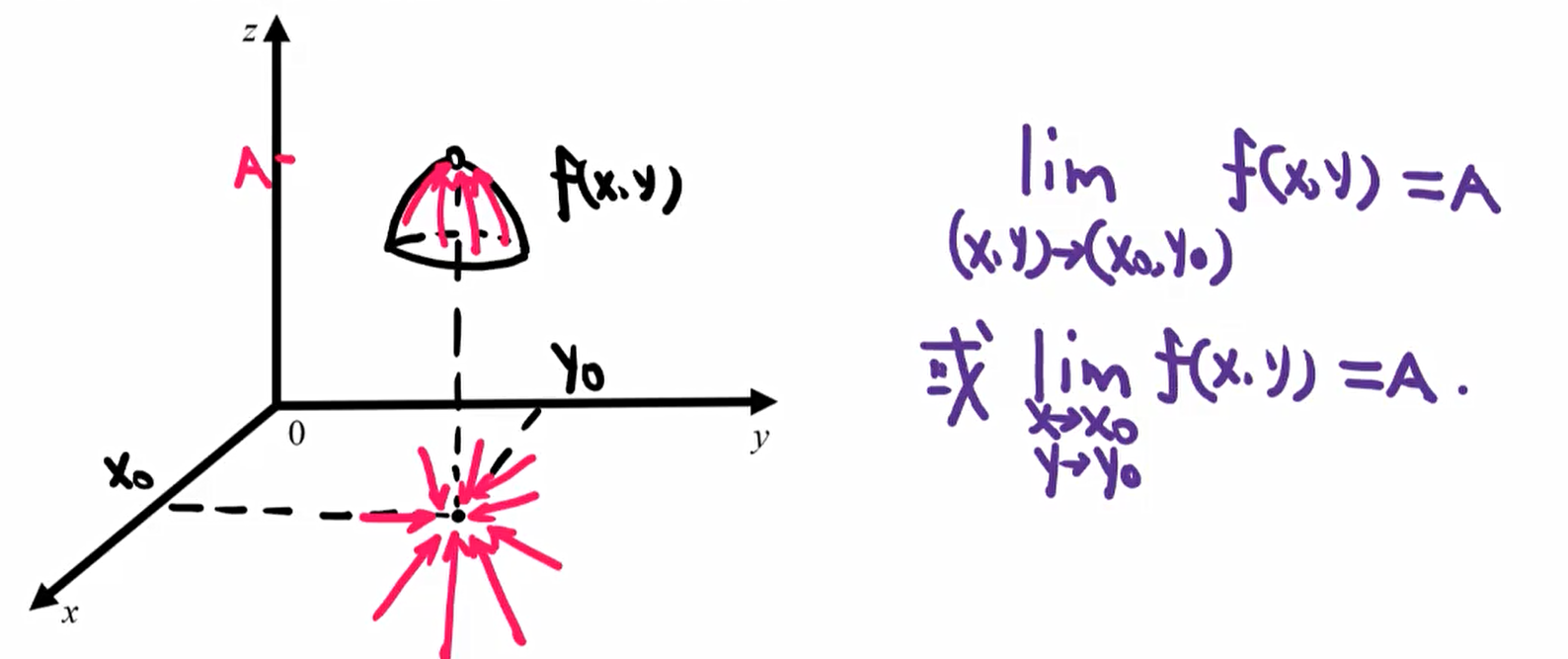
②二元函数极限

• 二重极限有无数条取向。

• 当确定某一条趋向后，二重极限将变成一个一重极限。

• 二重极限没有阶的概念。

二重极限不存在

• 找一条趋向下极限不存在

• 找两条趋向下极限不相等

  例如：$y=x,y=x^2,y=x^k,y=kx,x=y^2…$

二重极限存在

1. 定型
2. 等价无穷小
3. 整体代换变一重极限
4. 夹逼定理
5. 0*有界=0

③连续的判定✅

任何趋向下极限都等于函数值才连续。

④可导的判定✅

⑤可微的判定✅

2️⃣偏导数定义及计算

①定义

可导与连续之间无任何关系，可导推不了连续，不连续也不一定就不可导！

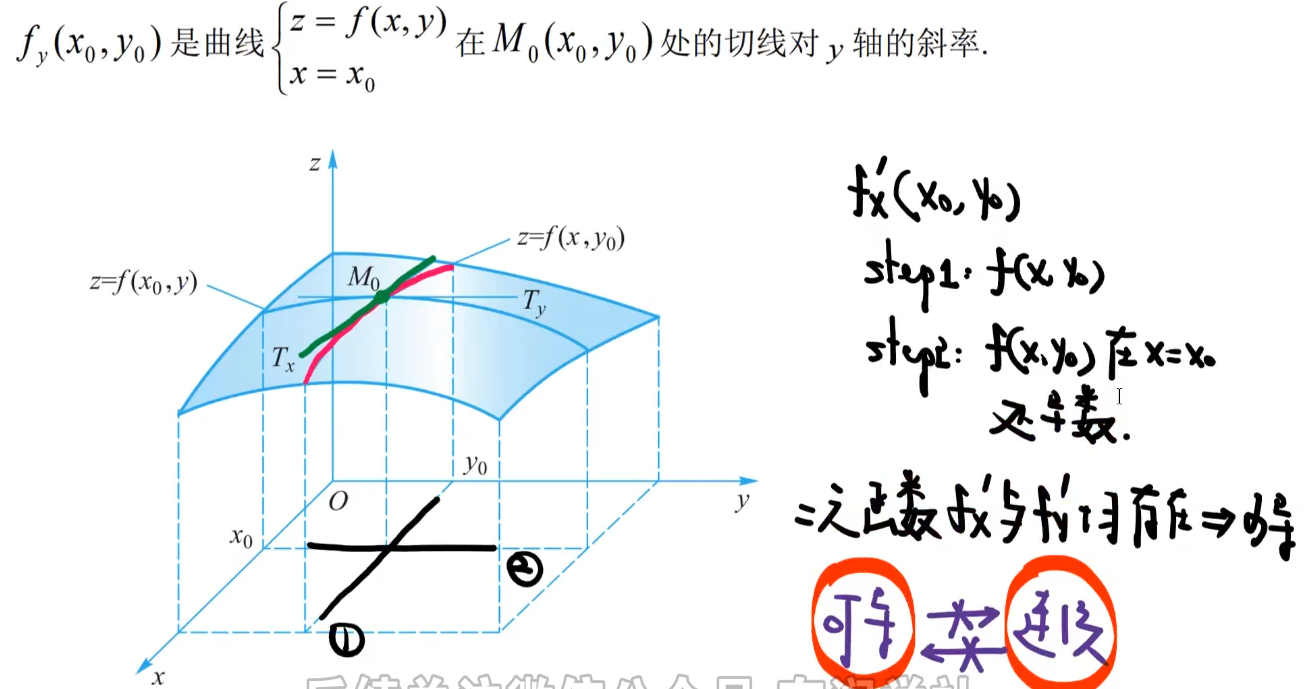
②几何意义

④计算

对某一个自变量求偏导，因为其余自变量看为常数，可以先代值再计算。例如：$\frac{{\partial}z}{{\partial}x}$ 和 $\frac{{\partial}z}{{\partial}y}$ 可以先代入 $y$ 和 $x$ ，$\frac{{\partial}^2z}{{\partial}x^2}$ 和 $\frac{{\partial}^2z}{{\partial}y^2}$ 可以先代入 $y$ 和 $x$ ，而 $\frac{{\partial}^2z}{{\partial}x{\partial}y}$ 和 $\frac{{\partial}^2z}{{\partial}y{\partial}x}$ 都不可以先代入，因为代入的话后面进行求导的话就变成常数了，但第二次对 $x$ 或 $y$ 求偏导的时候 $y$ 或 $x$ 就可以带进去了。

多元函数的高阶偏导数

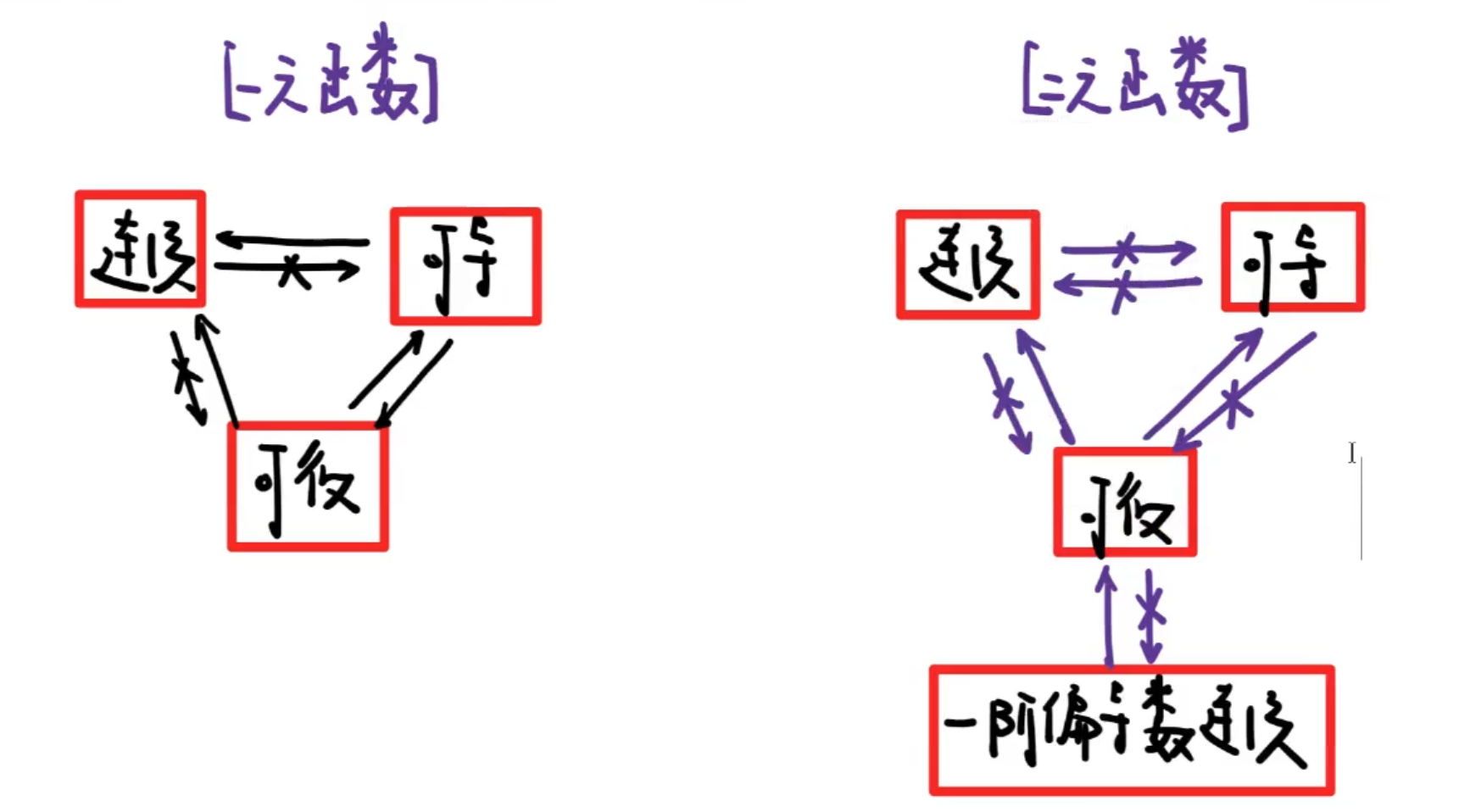
多元复合函数偏导数

先对中间变量求导，中间变量再对自变量求导，有多少个中间变量就有几个部分。

单中间变量（复合函数）

直接依次求导，不可能出现角标。

多中间变量

3️⃣全微分

可微、可导、连续♻️

4️⃣二元隐函数

①求导

两边同时求导

方程两边同时对 $x$ 或 $y$ 求偏导，注意 $z$ 中有 $x$ 和 $y$

公式法

②隐函数存在定理

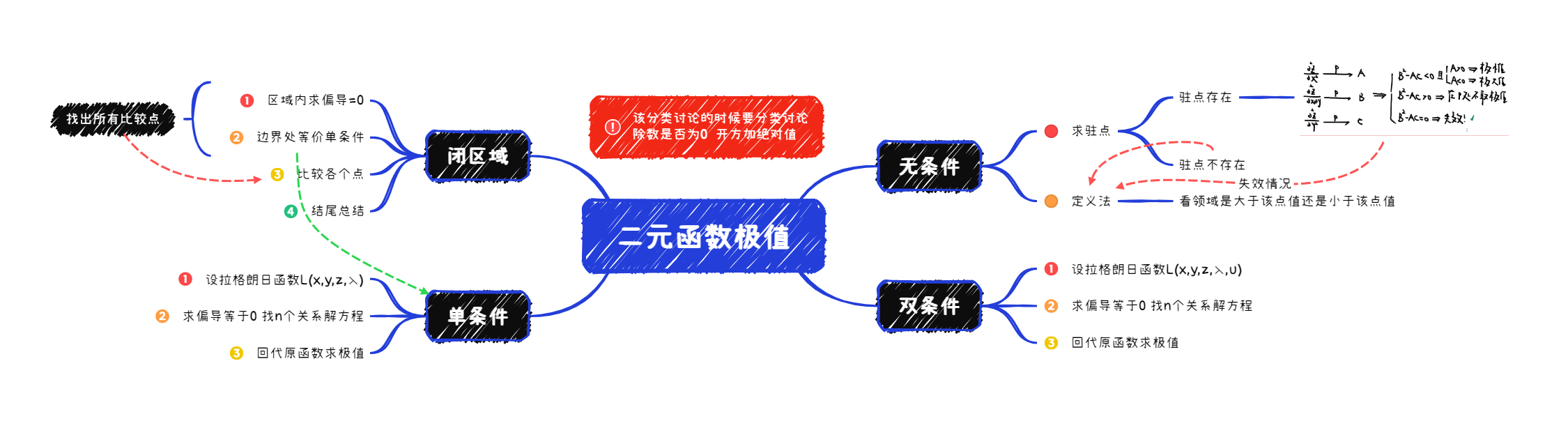
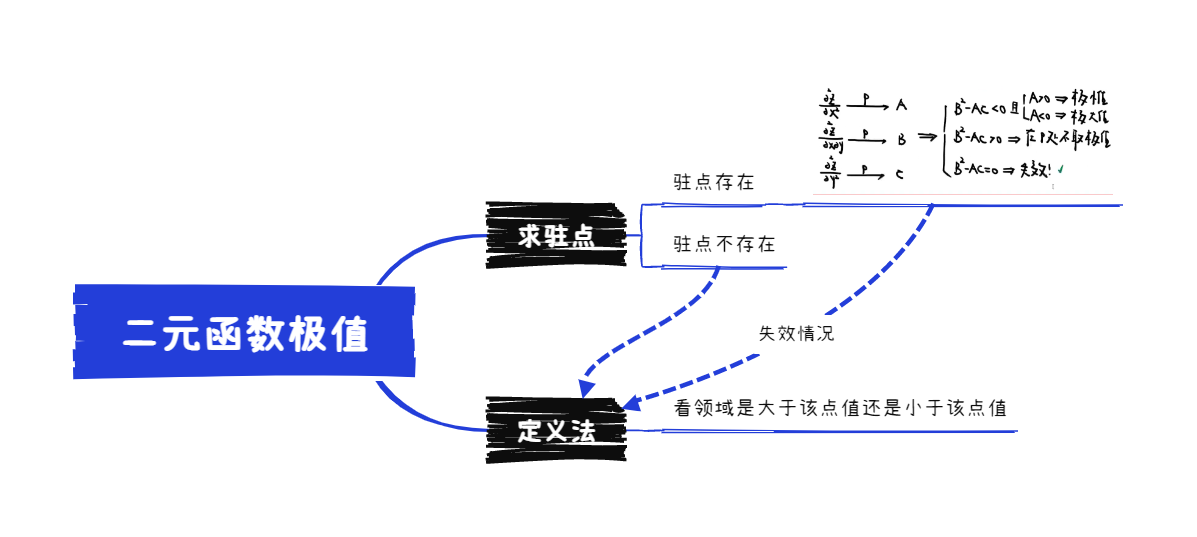
5️⃣二元函数极值

①定义

领域内都大于或小于该点的值。

②可疑点

• 驻点
• 不可导点（两个偏导一个不存在就是不存在）

③求解

无条件极值

单条件极值

双条件极值

二元函数闭区域最值

边界上回到单条件极值求解。

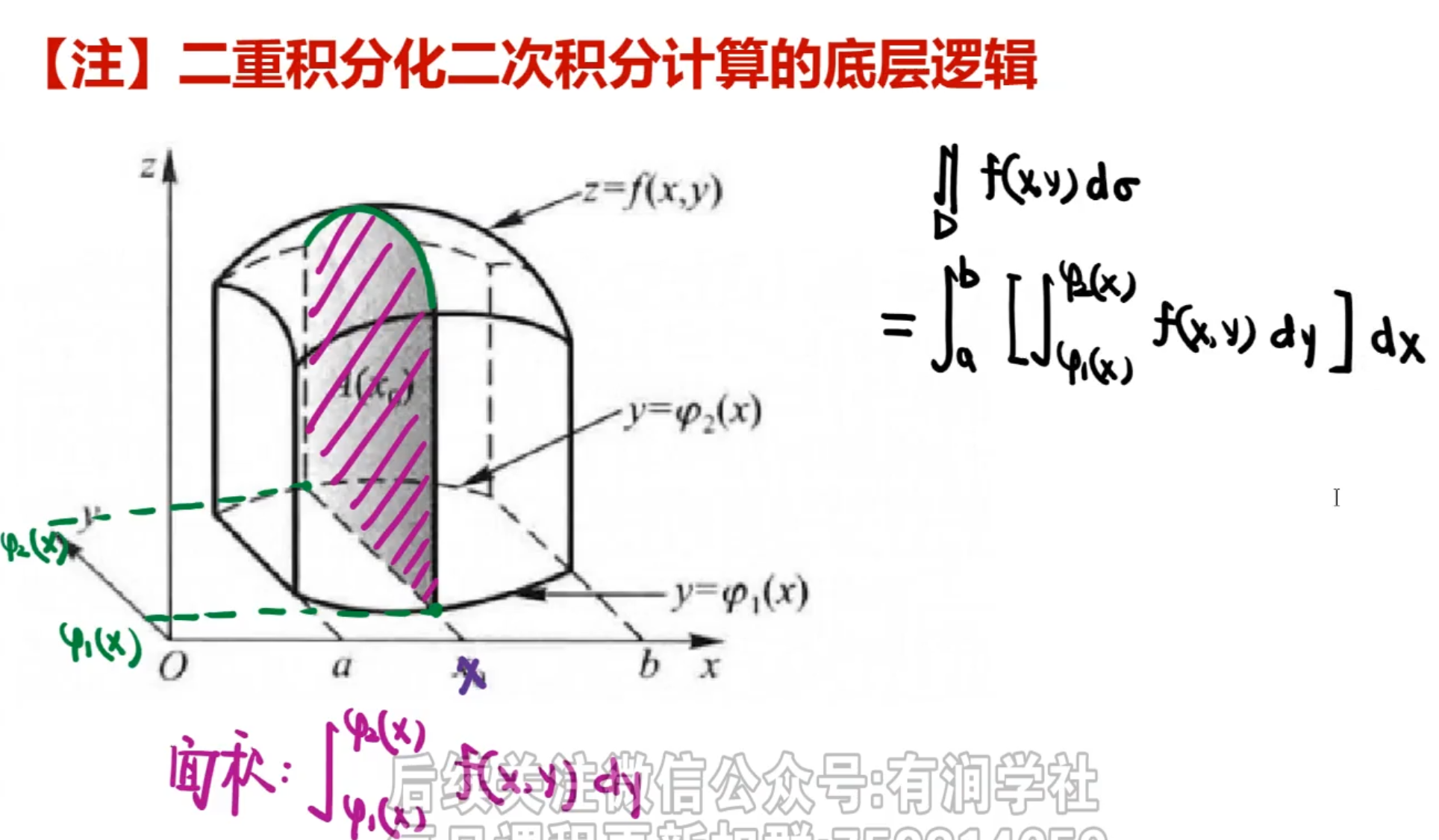
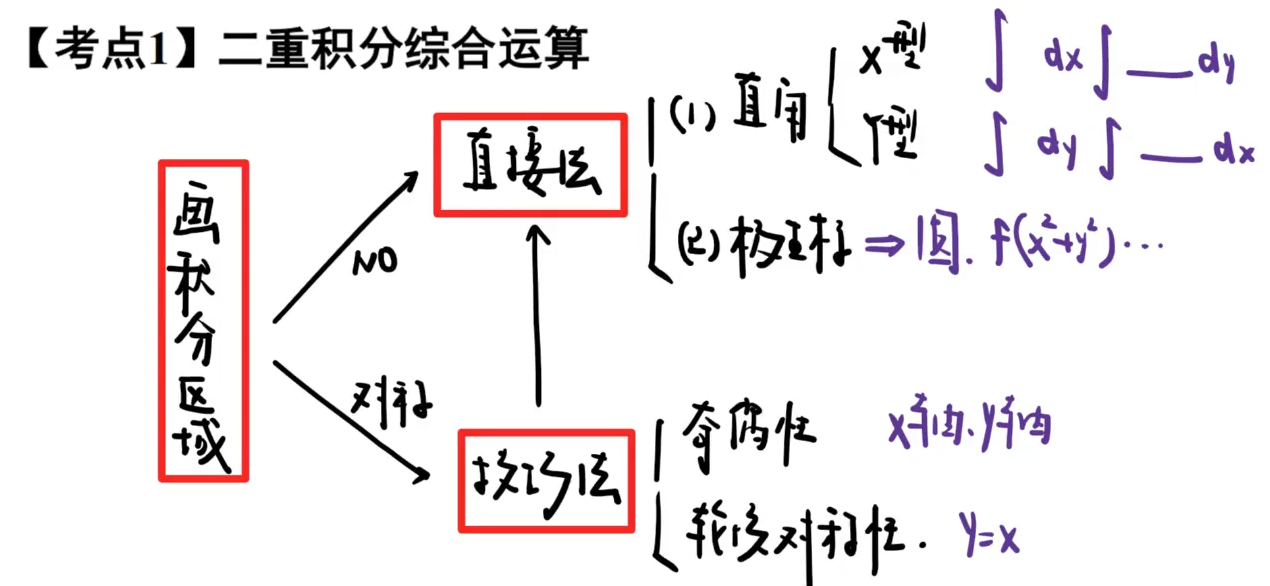
二重积分

1️⃣几何意义

2️⃣计算方法

①直接法

直角坐标系化二次积分

取点、划线、投影、积分

极坐标系化二次积分

该用极坐标的时候一定要用，否则不是麻不麻烦的事情，有可能真的解不出来！！！

②技巧法

区域对称性（X、Y）

关于$x$对称的话把$x$看成常数后后看$y$的函数，偶倍奇零。

轮换对称线

积分区域关于 $y=x$ 对称，那么被积函数的 $x$ 和 $y$ 互换后值不变。

调换积分次序

dx中下限和上限对应左右，dy中下限和上限对应下和上。

③雅可比换元法

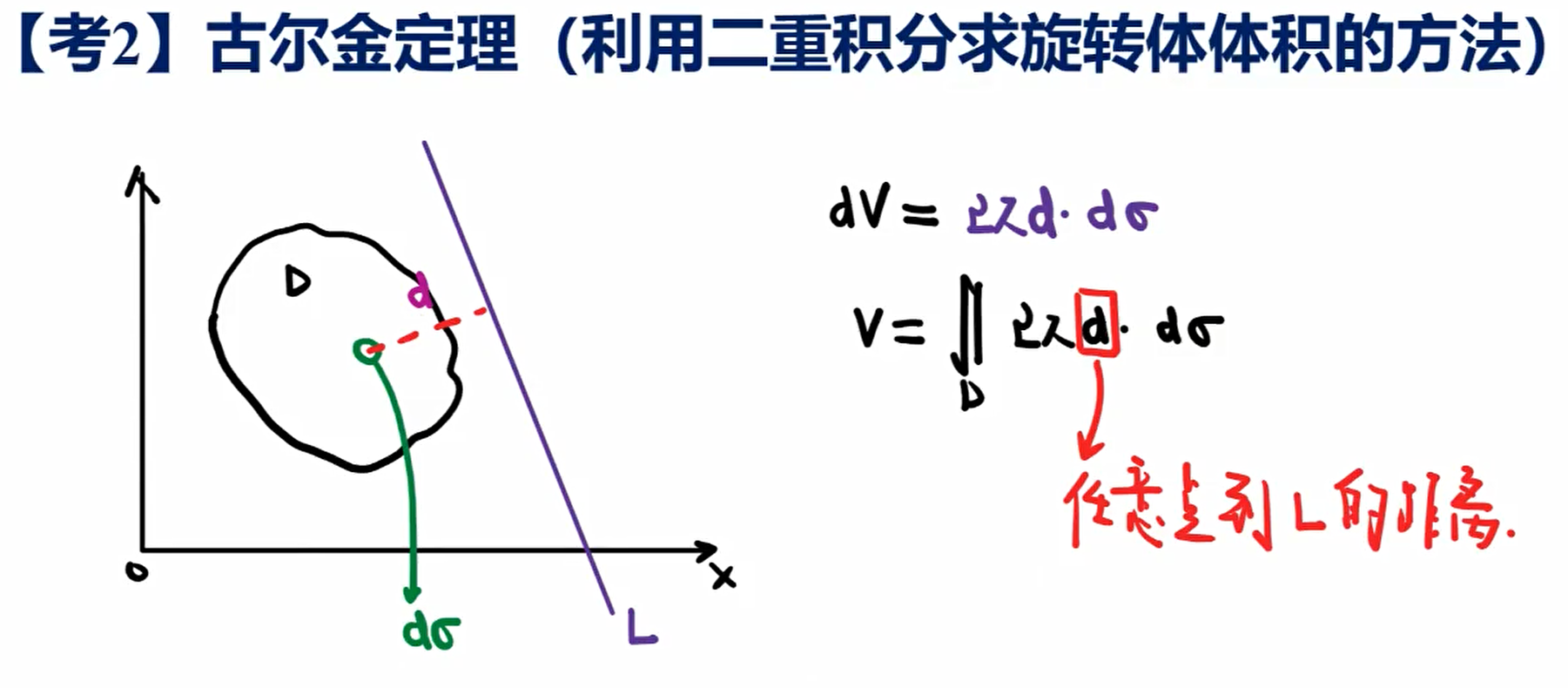
④古尔金定理

行列式

1️⃣基本概念

①定义

1. 行列式是来自不同行不同列元素乘积的代数和。
2. 行列式本质上是一个数。
3. 行列式是一个运算法则。
4. 行列式是一个双竖线里面加了一个方针，行数=列数。

②行列式计算

二阶和三阶适用。

③n阶行列式

④特殊的行列式

主对角线形

副对角线形

2️⃣行列式的性质

1. 行列式与它的转置行列式的值相等。

2. 互换行列式的两行（列），行列式变号。

3. 若行列式某行（列）有公因子k，则可把公因子k提到行列式外面。

4. 若行列式有两行（列）完全相同或成比例，则此行列式等于零。

5. 行列式的某一列（行）的各元素乘以同一数然后加到另一列（行）对应的元素上去，行列式不变。

6. 若行列式的某一列（行）的元素都是两数之和，则此行列式等于两个行列式之和。

   

3️⃣余子式

行列式展开定理

行列式等于它的任一行（列）的各元素（系数）与其对应的代数余子式乘积之和。

行列式线性和

推论：某一行的元素乘另外一行对应的代数余子式和为零。

4️⃣特殊的行列式

范德蒙行列式

abcd从0次方到n-1次方（一定有一排1）等于后面依次减前面

行（列）和相等形

提出来化对角

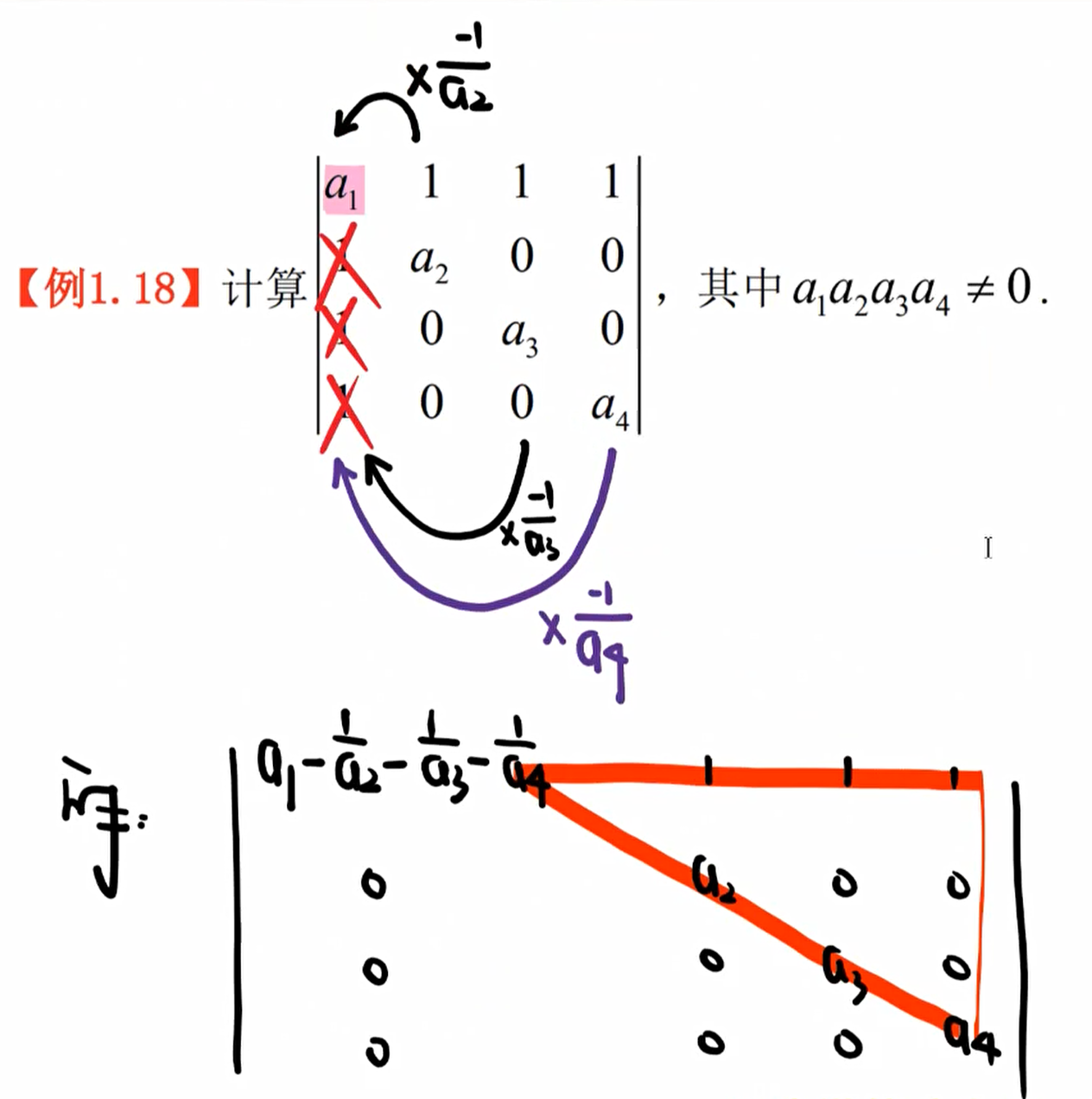
爪形行列式

干掉一排爪子

点斜行列式

按第一列展开

三线行列式⭐️

线性递推式的求解

二阶线性地推式

数学归纳法

第一类数学归纳法

第二类数学归纳法

求特征值

对应消零成比例，行一下列一下

矩阵

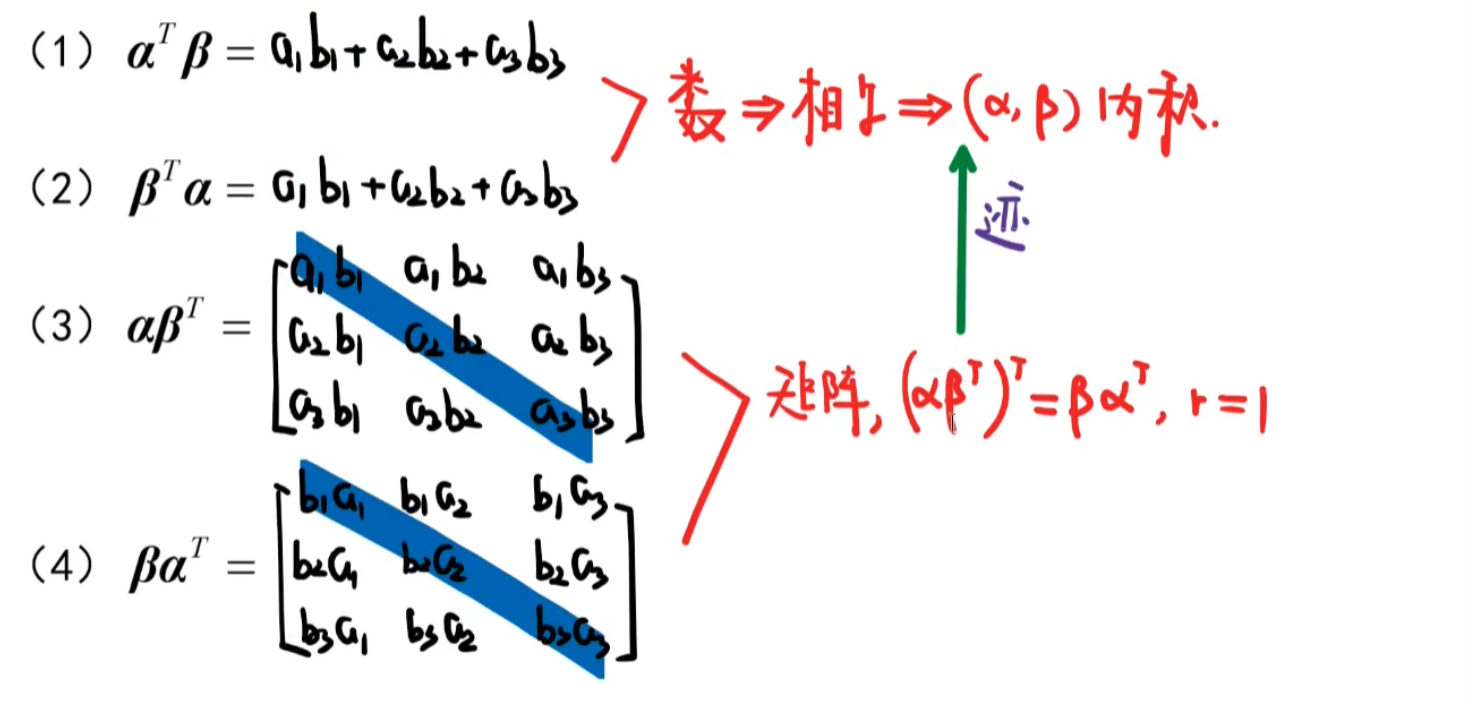
1️⃣基本运算

1. 矩阵乘法没有交换律：$AB≠BA$

2. 矩阵乘法没有零因子律：$AB=0\not\rightarrow{A=0

   B=0}$，只能推出$

   A

   =0或者

   B

   =0$

3. 矩阵乘法没有消去律：$AB=AC\&\&A\neq0\not\implies{B=C}$

2️⃣转置矩阵

性质

1. $(A^T)^T=A$
2. $(kA)^{\mathrm{T}}=kA^{\mathrm{T}}$
3. $(AB)^{\mathrm{T}}=B^{\mathrm{T}}A^{\mathrm{T}}$
4. $(A+B)^{\mathrm{T}}=A^{\mathrm{T}}+B^{\mathrm{T}} $

对称矩阵

两矩阵可交换

方阵的行列式

1. $

   A^{T}

   =

   A

   $

2. $

   kA

   =k^{n}

   A

   $

3. $

   A\pm B

   \neq

   A

   \pm

   B

   $

4. $

   AB

   =

   A

   \cdot

   B

   $

5. $

   A^*

   =

   A

   ^{n-1}$

6. $

   A^n

   =

   A

   ^n$

7. $A^k*A^l=A^{k+l}$
8. $(A^k)^l=A^{kl}$

9. $(A^*)^{-1}=\frac{A}{

   A

   }$

3️⃣伴随矩阵（方阵）

万能公式

\[A*A^*=A^**A=|A|E\]

1. 各个元素代数余子式最后要转置。
2. 代数余子式要带正负号。
3. 二阶伴随：主对调，副换号。

4️⃣逆矩阵（方阵）

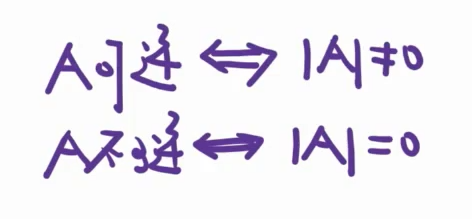
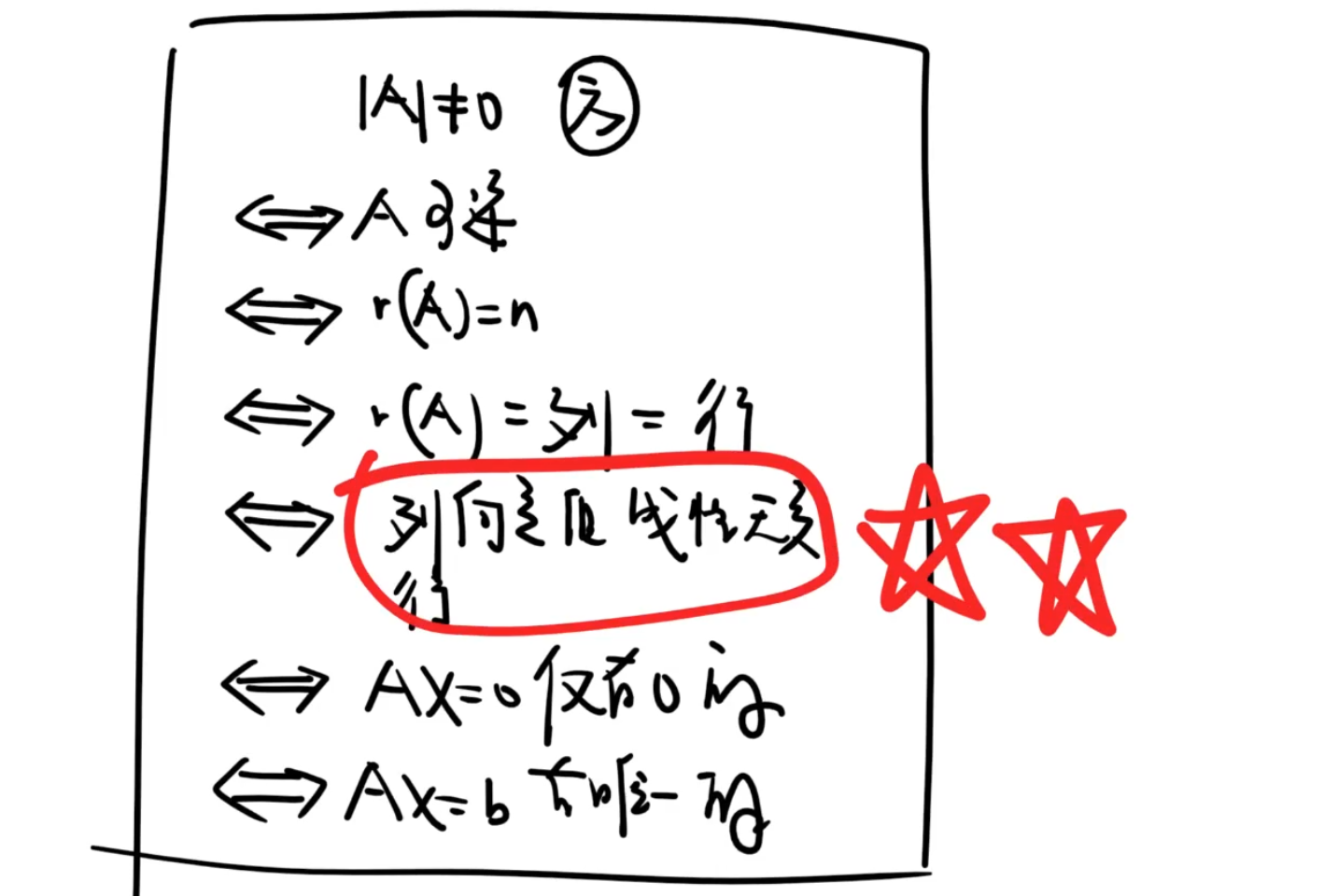
矩阵可逆的充要条件

逆矩阵的求解

抽象型

• 定义法
• 

数值型

• 公式法
• 初等变换法
• 分块法

逆矩阵的性质

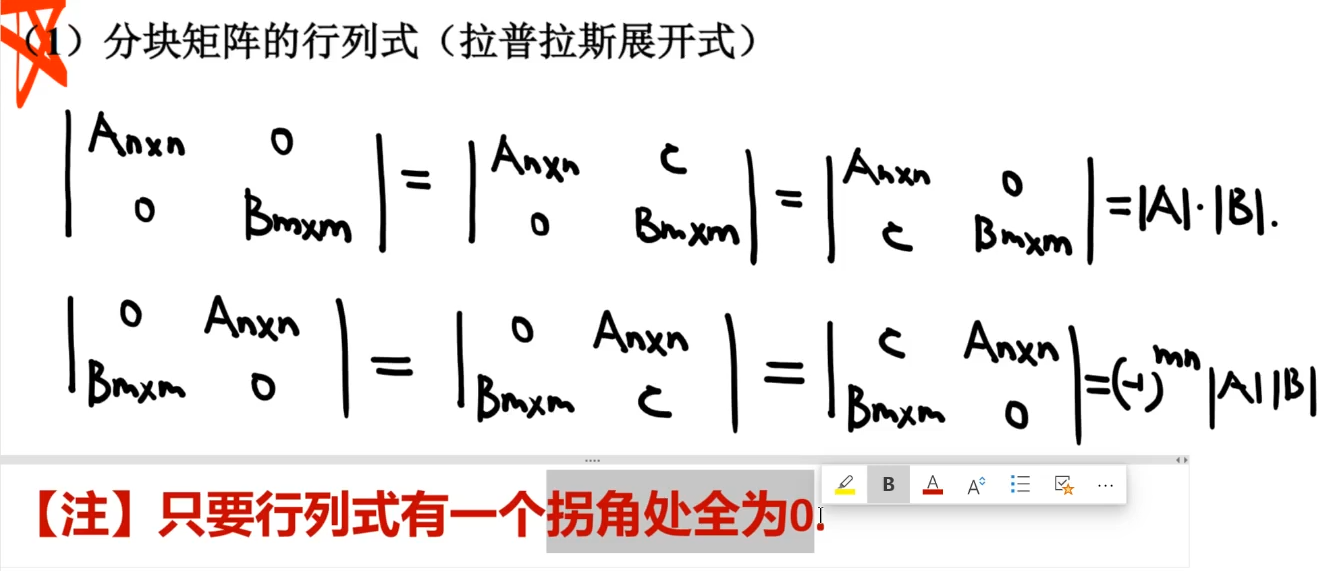
5️⃣分块矩阵

拉普拉斯行列式

注意两边都是零。

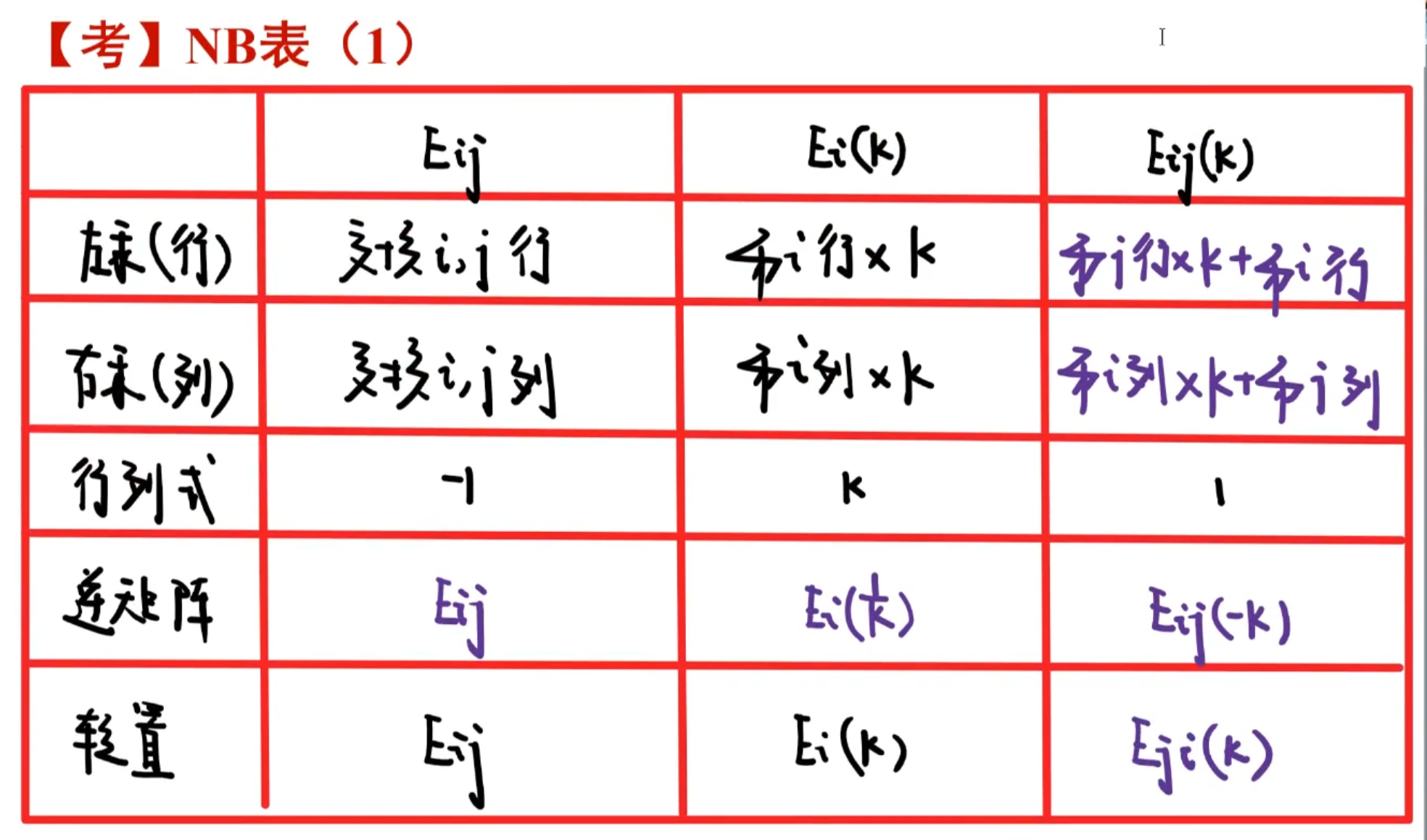
7️⃣初等矩阵

【左行右列】初等矩阵与初等变换之间的关系：

左行：左乘初等矩阵，相当于让该矩阵进行一次相应的行变换 右列：右乘初等矩阵，相当于让该矩阵进行一次相应的列变换

行就近列就远。

6️⃣矩阵等价

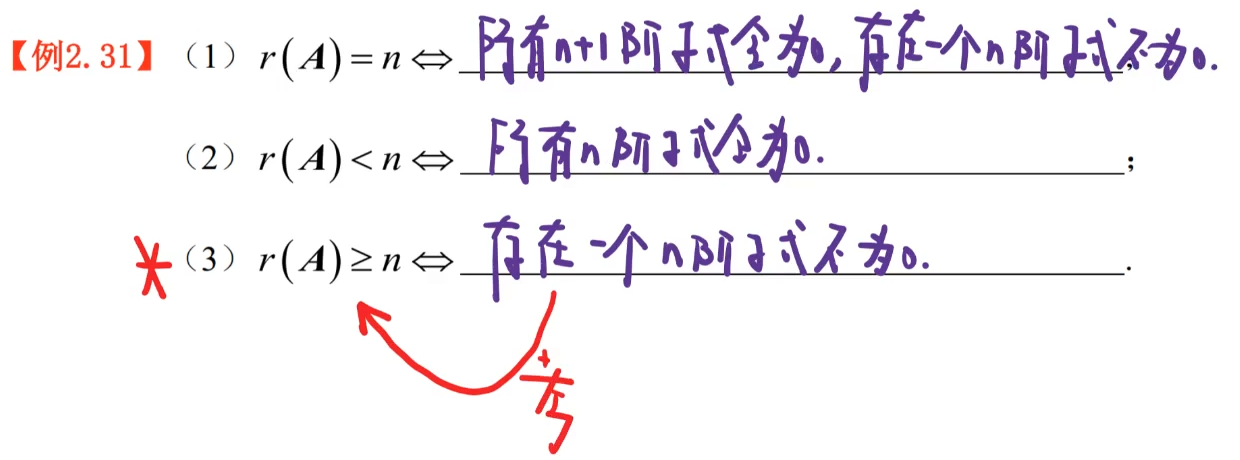
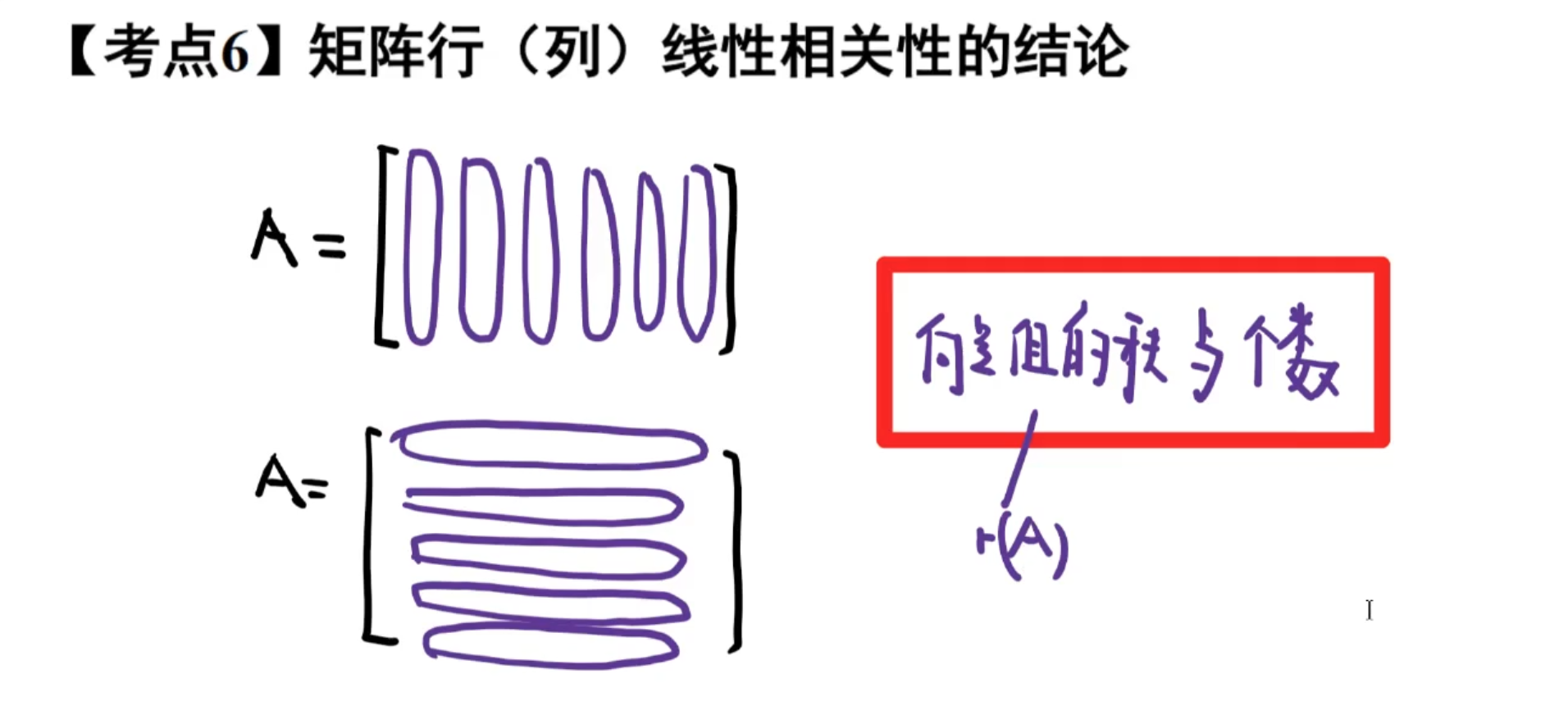
6️⃣矩阵的秩

两行消不掉

求矩阵的秩

• 利用矩阵秩的定义
• 利用初等变换化行阶梯矩阵求秩（行、列）
• 利用行列式（方阵）

分类讨论的情况

所见之处都要分类讨论。

常用公式

对于mxn的矩阵，有：

伴随矩阵A*的秩

分块矩阵的秩

矩阵等价

向量与方程组

线性相关

等价说法

局部与整体的关系

判断线性相关性

定势思维：

定义法

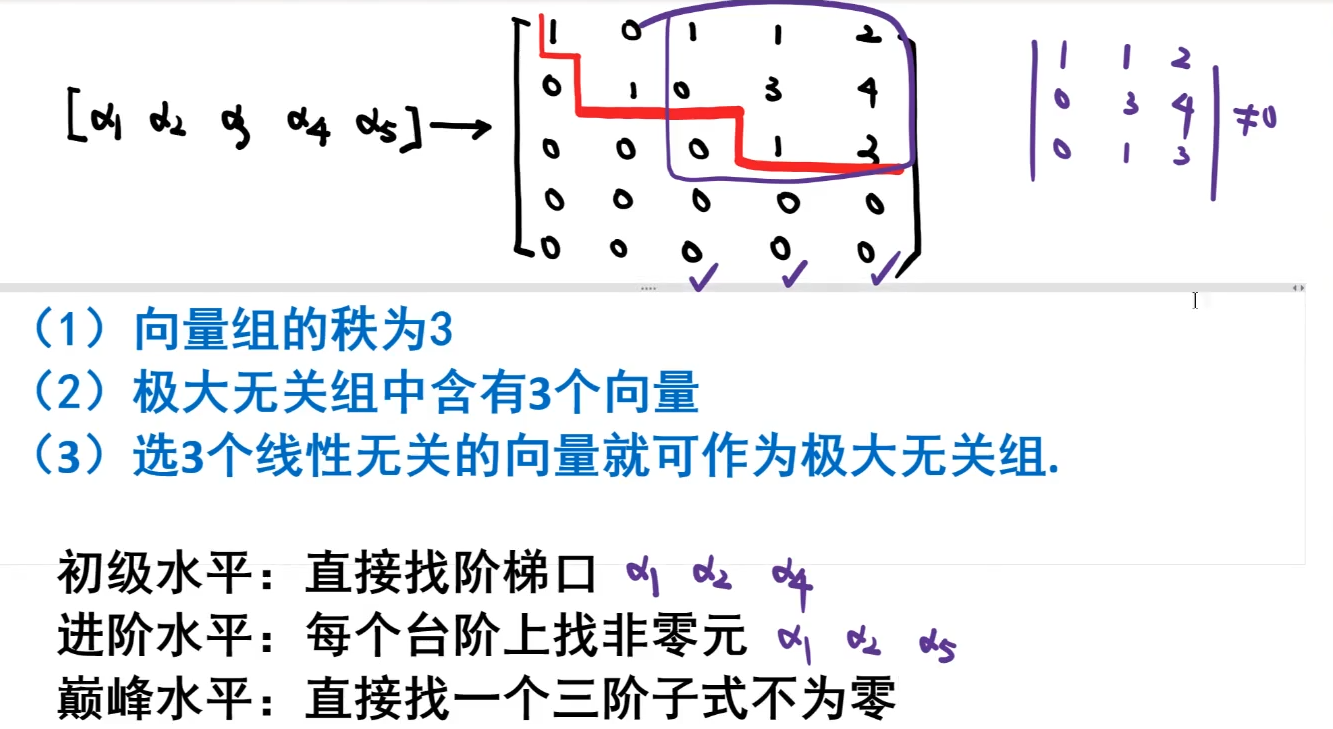
向量组的秩

判断行列向量组相关性

核心思想是秩和个数相比，行秩和列秩都相等

极大无关组

向量的秩

向量组的秩=列向量的秩=行向量的秩

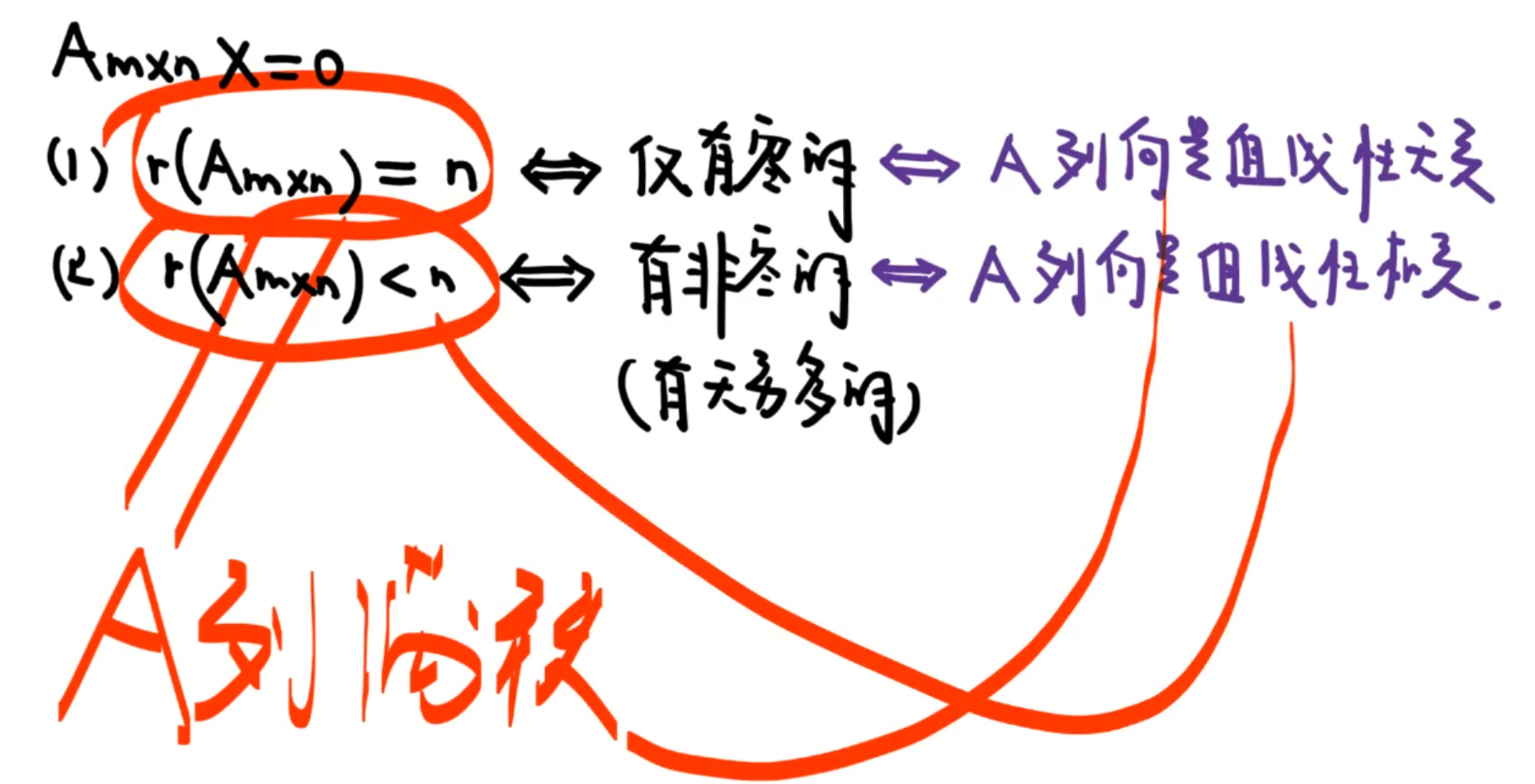
齐次线性方程组

通解形式

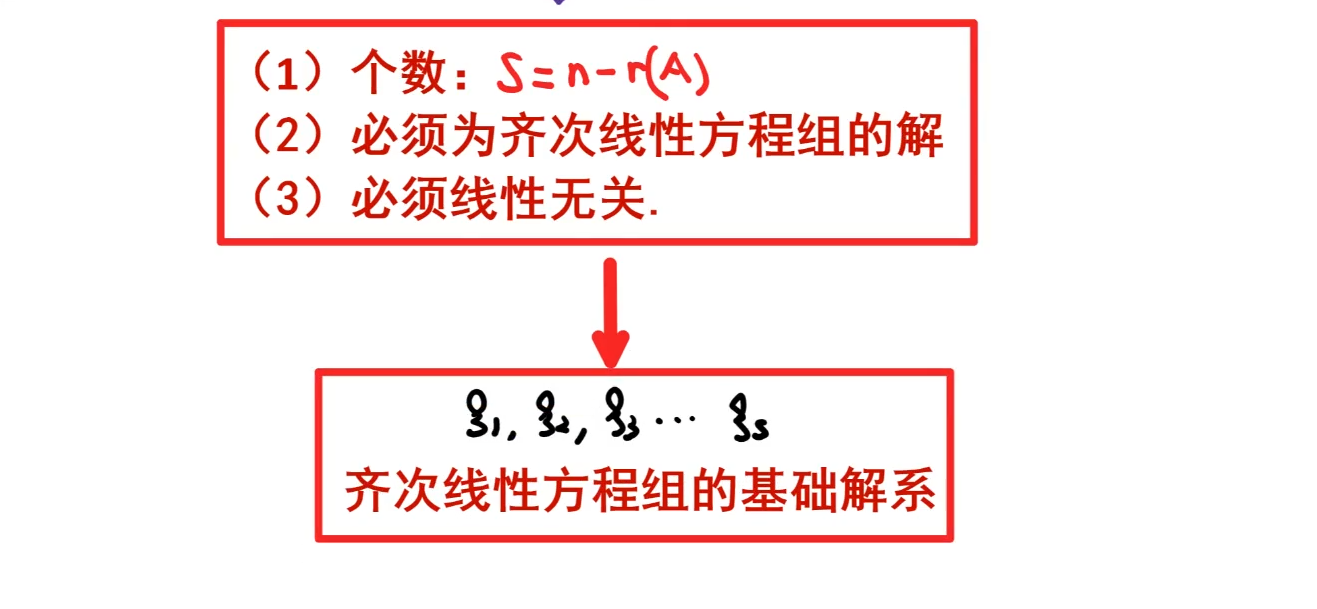
基础解系

最多有s个线性无关的解。

判定条件：

• 个数s等于n-r
• 线性无关
• 是方程组的解

非齐次线性方程组

表达形式

解的判定

基础解系

最多有s+1个线性无关的解。

为什么要化行阶梯矩阵： 把主元化成自由之后，系数矩阵是EF，要让AN=0，所以N就是-F/E，此时-F就是特解，加个常数表示所有特解就是通解

克拉姆法则

系数矩阵必须是方阵，要求行列式不为零=>方程有唯一解。

在使用克拉姆法则判断解的情况时候，如果行列式为零，可能是无解也可能是无穷解，需要检验*

线性表示

矩阵方程

表达形式

解的判定

线性表示

向量组等价

定义

【注1】一个向量组与其极大无关组是等价的

【注2】向量组等价无须要求向量组内向量个数相同

判定

特征值

1️⃣特征值与特征向量

①定义

②求解特征值和特征向量

数值型矩阵

求解特征值

【特殊矩阵】主对角线型矩阵的上三角、下三角、对角阵的特征值均为对角线上元素

求解特征向量

抽象型矩阵

求解特征值

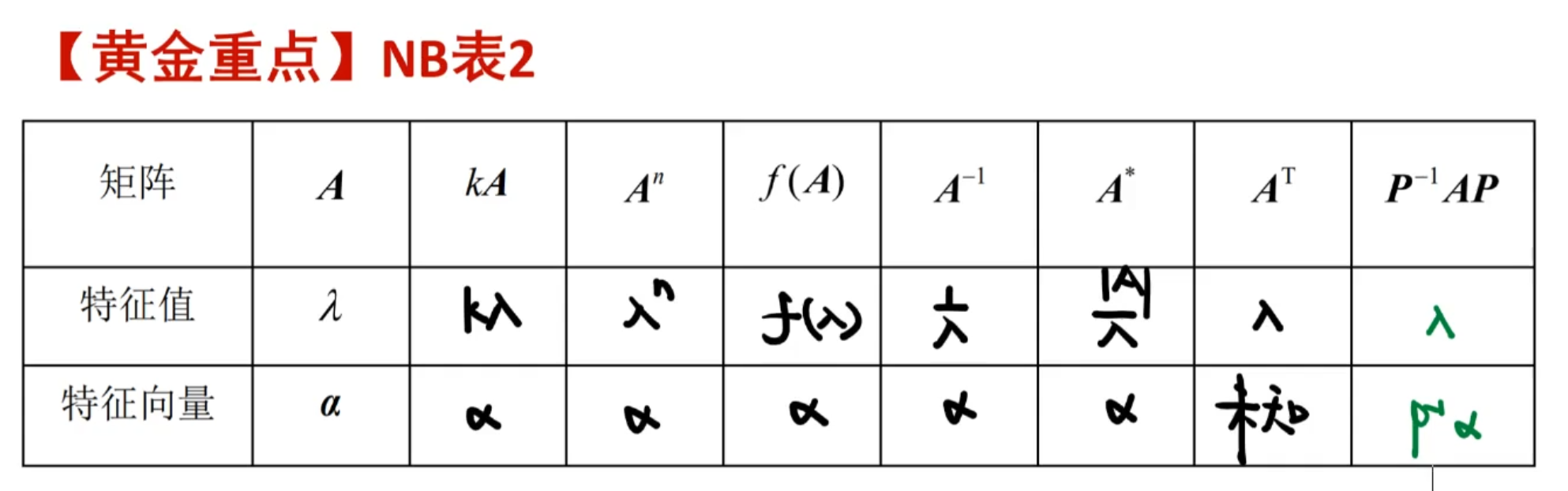
NB表二

已知A的特征向量求伴随的特征向量的小技巧：

③特征值的性质

• 行列式的值为特征值的乘积
• 矩阵的迹为特征值的加和

④特征向量的性质

• 不相同特征值对应的特征向量线性无关
• 相同特征值对应的特征向量可能线性相关，也可能线性无关
• k重特征值最多对应k个线性无关的特征向量，最少对应1个线性无关的特征向量（例如三重根的解空间可以是线可以是面可以是体）
• 若$\alpha$是矩阵A的特征向量，则$k\alpha$也是矩阵A的特征向量

2️⃣矩阵相似

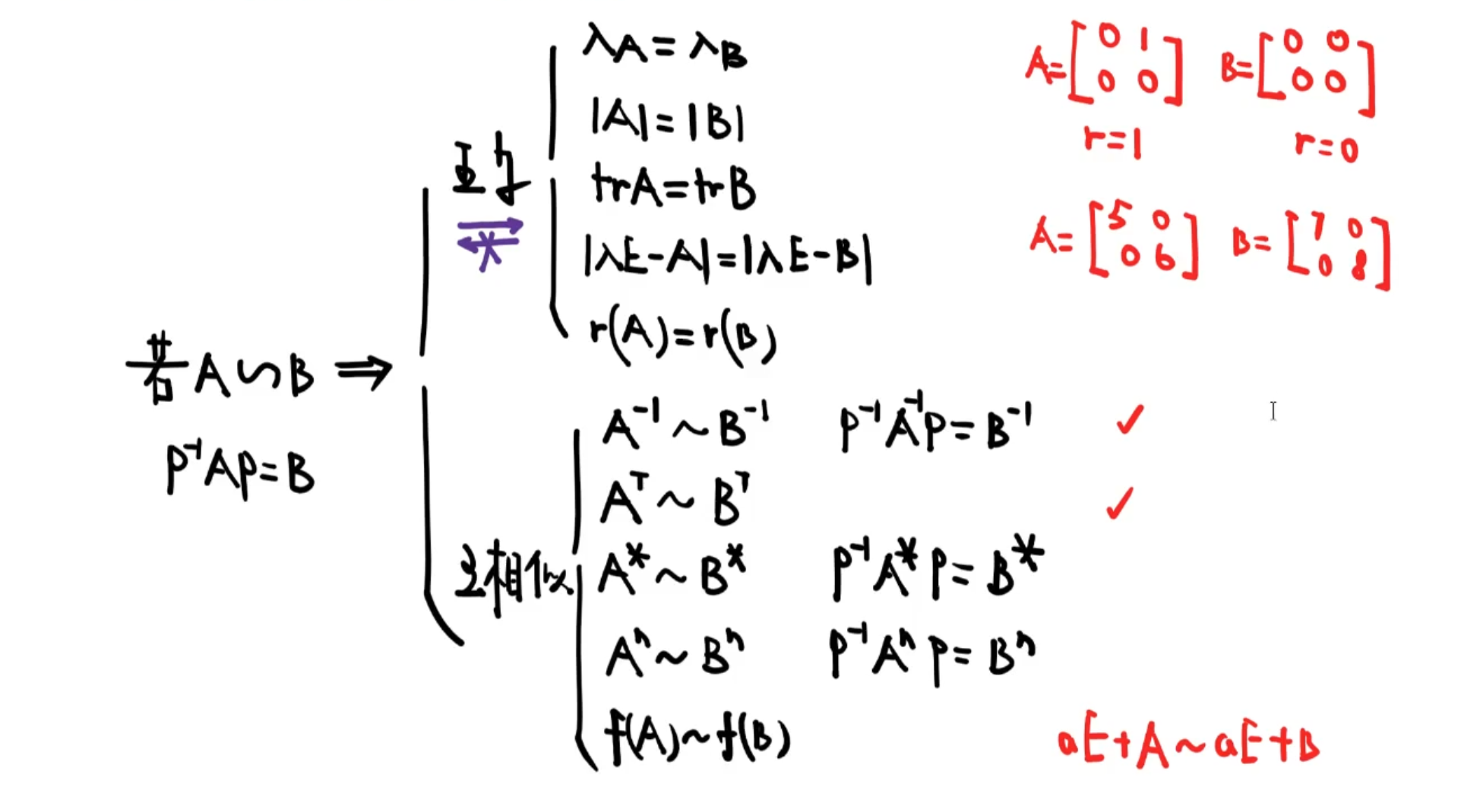
①相似定义

注意：初等行列变换后矩阵不再相似

②相似性质

定势思维

零矩阵的特征值都是0，设A的特征值λ=0

③相似对角化定义

就是一种特殊的相似情况

④相似对角化性质

当矩阵可以相似对角化时，矩阵的非零特征值的个数等于矩阵的秩。

⑤相似对角化应用

求A的时候：

【1】方法一的缺点是需要求逆矩阵

【2】正交化（反求A的时候逆就是转置）单位化（求n次幂只有单位化后才可以消掉）

求A的n次幂的时候：

对角阵n次方后就是一个数，然后$P或Q$和$P^{-1}或Q^{-1}$可以消掉，两者无差别

⑥相似对角化变换

变换特征向量

变换特征值

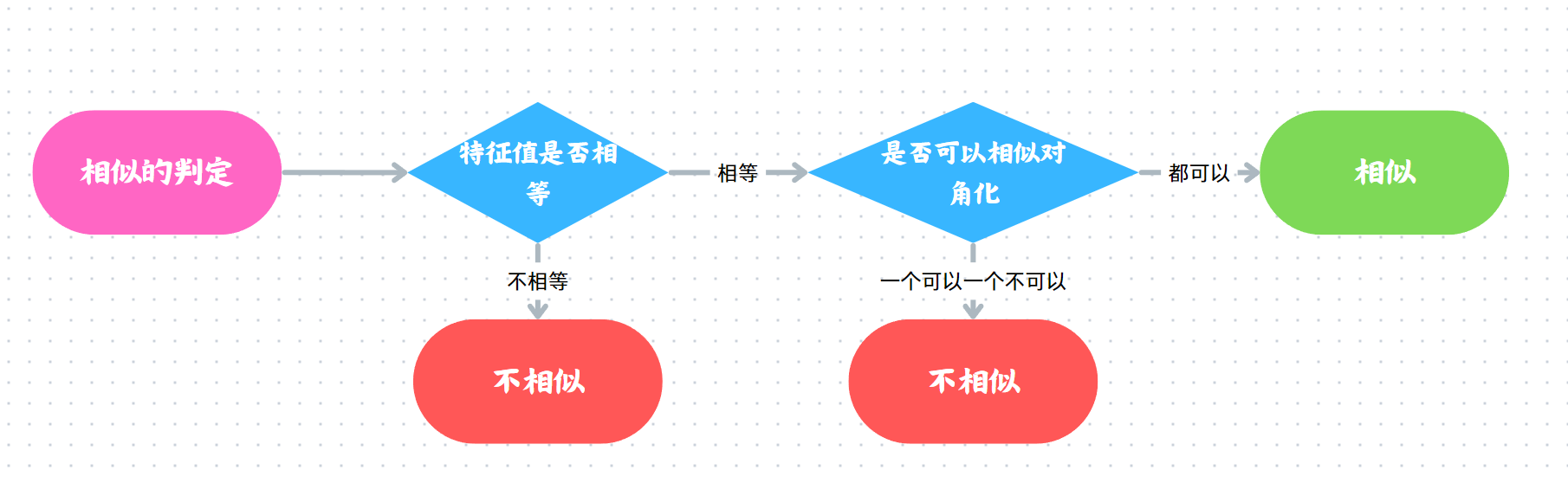
⑦相似对角化的判定

必要条件

• R重根是否有R个线性无关的特征向量
• A有n个线性无关的特征向量
• 对每个i重特征值λ，r(λE-A)=n-i（和上面条件一个意思，适用于选择题）

充分条件

• A具有n个不同的特征值
• A为实对称矩阵

向量基础知识（补）

正交矩阵

正交矩阵定义

对于n所方阵而言，若$AA^T=E$，则A为正交矩阵。

正交矩阵性质

• $A^{-1}=A^{T}$

• $AA^{-1}=A^{-1}A=E$

• $AA^{T}=A^{T}A=E$

• 矩阵的每一个列向量均为单位向量

• 矩阵的列向量间是正交的

另一种表达法：

3️⃣实对称矩阵相似对角化

①实对称矩阵

$λE-\alpha{\alpha}^T$是对称矩阵

实对称矩阵性质

• 实对称矩阵一定存在正交矩阵使得该矩阵相似对角化

• 实对称矩阵的r重特征值一定具有r个线性无关的特征向量（由上面一条可以推出）

• 实对称矩阵的特征值均为实数

• 实对称矩阵不同特征值对应的特征向量是正交的（对于一般的矩阵是线性无关的）

题型

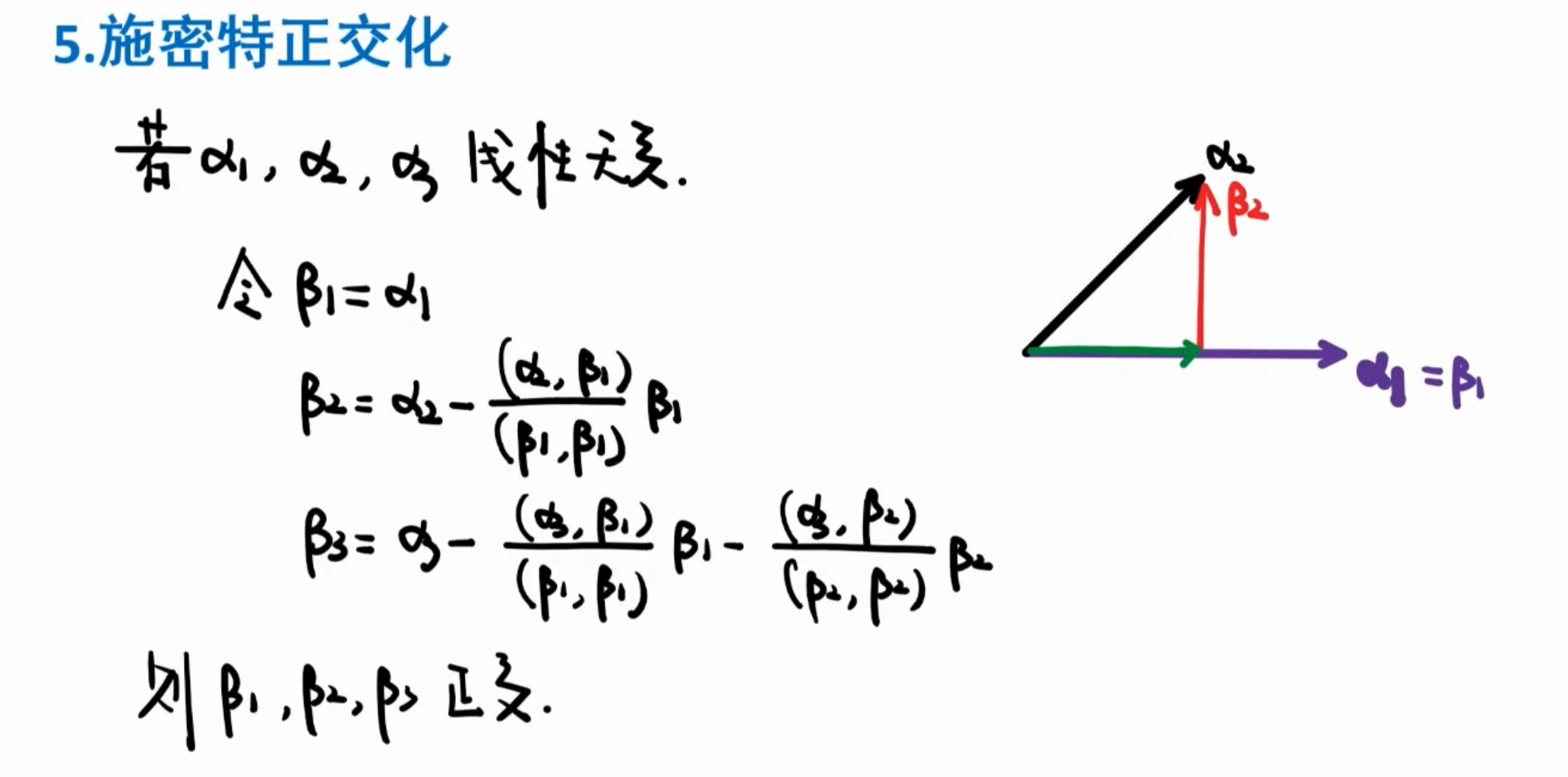
【题型】求一个正交矩阵，使实对称矩阵相似对角化

【解法】求出特征值和特征向量=>正交化=>单位化

正交化可在解特征向量时解出正交解：

②秩为1的矩阵

转置在前是数，转置在后是矩阵。矩阵的迹是数，也就是内积，而且秩为1

特征值

充要条件

对角化判定

二次型

1️⃣二次型及其对应矩阵

二次型的对应矩阵对应二次函数的系数，必须对半分，所以必须为实对称矩阵，因此矩阵和二次型一一对应。

	函数	对应矩阵
一般形	平方项➕交叉项	实对称矩阵
标准型	平方项	对角矩阵
规范型	平方项	对角矩阵的系数为1、-1、0

2️⃣矩阵合同

题目中出现合同，该矩阵一定是实对称矩阵。

①定义和性质

• 二次型经过可逆线性变换，前后矩阵是合同关系
• 二次型经过可逆线性变换，标准型不唯一（而且可以互相转换）
• 二次型经过可逆线性变换，正负惯性指数始终不变（合同签的就是这个）

②二次型化标准形

法1：正交变换法

二次型经过可逆线性变换，变成新的二次型，两二次型对应矩阵是合同关系

法2：配方法

配方法务必要保证线性变换是可逆的，只有是可逆的时候，二次型前后对应的矩阵才是合同的。

先凑$x_1$把$x_2$$x_3$当常数，再凑$x_2$把$x_3$当常数，最后凑$x_3$，凑的时候以杂交项凑，因为最后会剩平方项

【线代必看！彻底搞懂配方法化二次型为标准形！全网最形象！】

如果没有平方项，固定设👇下面 的等式创造平方项

③惯性定理

求二次型的正负惯性指数

• 正交变换后看特征值
• 配方法后看系数

如何求二次型的规范型

1. 求出标准型
2. 将标准型的系数放到平方里面再进行换元

③正定二次型

正定二次型的定义

对于${\forall}A≠0$，有$f=x^TAx>0$。

正定二次型的判定

正定矩阵一定是对称阵——要想检验为正定矩阵，必须先检验为对称矩阵

充要条件

1. ${\forall}A≠0$，$f=x^TAx>0$
2. $λ_i>0$
3. $p=n,q=0$
4. 存在可逆矩阵P，$P^TAP=E$（正交变换后是单位阵，与单位阵合同）
5. 存在可逆矩阵D，$A=D^TD$（上一章反求A的思路）
6. A的所有顺序逐子式大于0。

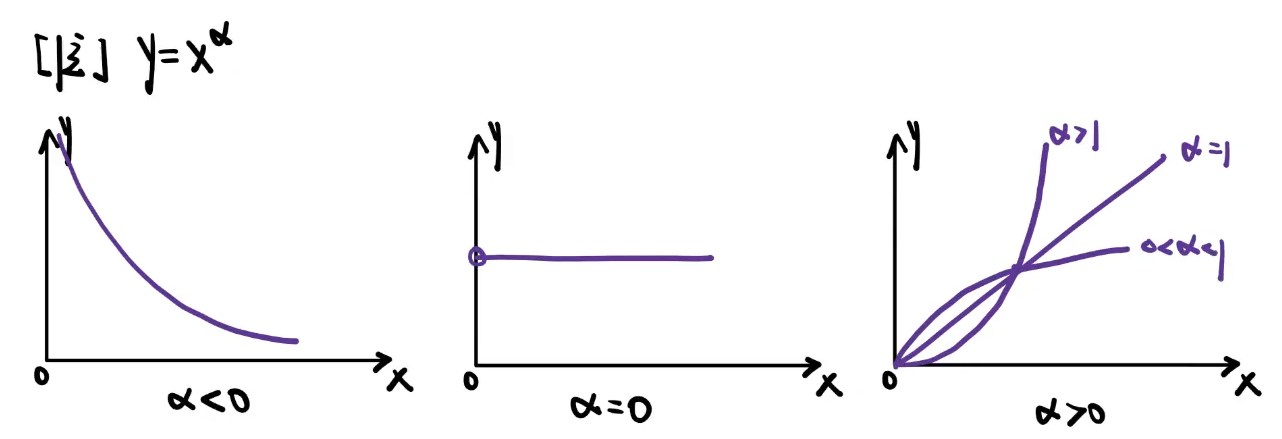
附录1【函数图像专题】

函数图像变化规则

左加右减，下加上减。往往的左加右减，上加下减是因为那是对于一次函数$y=ax+b$，把b移到跟y一边就是$y-b=ax$，所有是下加上减。

常见图像

附录2【常见函数导数积分表】

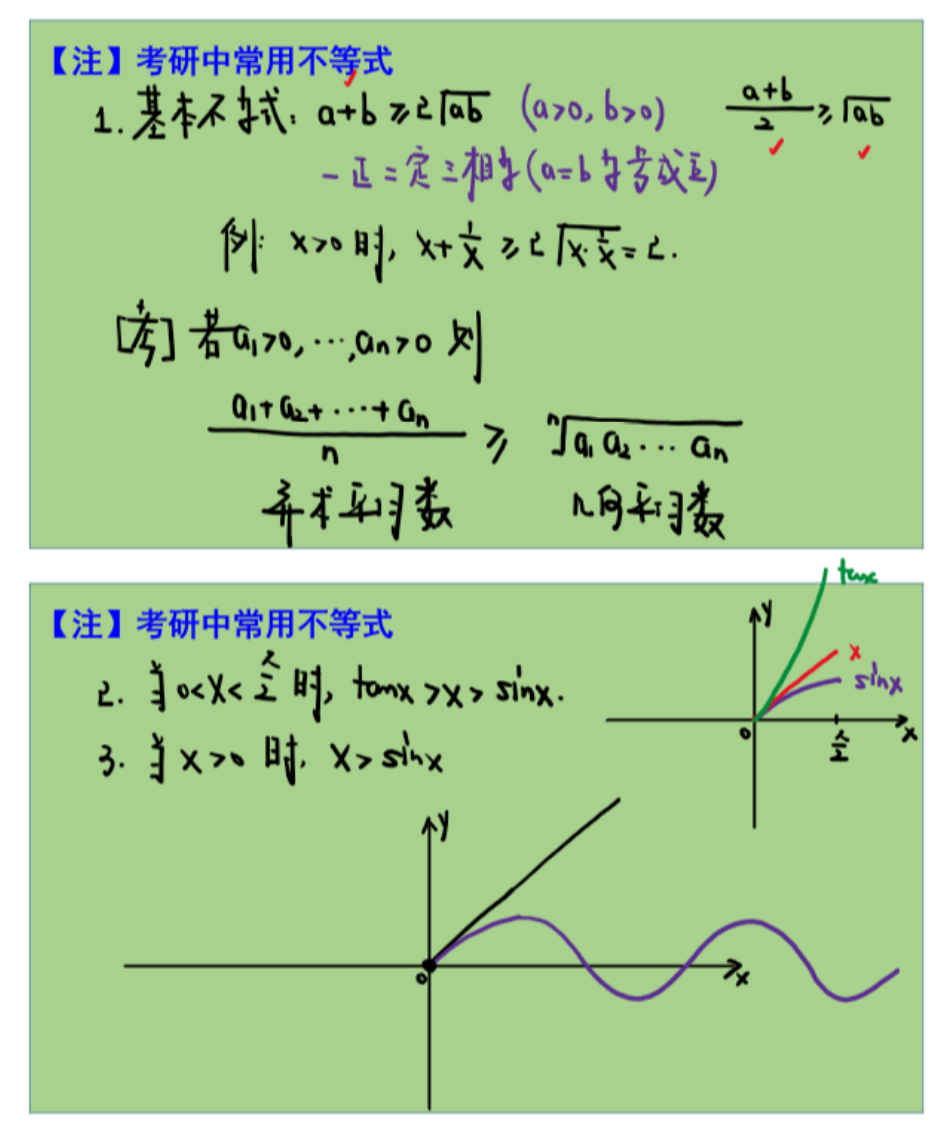
附录3【常考不等式】

附录4【等价无穷小】

以下公式可以整体代还，包括次幂

$x$	$x^2$	$x^3$
$sinx{\sim}x$	$1-cosx{\sim}{\frac{1}{2}}x^2$
$arcsinx{\sim}x$
$tanx{\sim}x$
$arctanx{\sim}x$
$ln(1+x){\sim}x$
$e^x-1{\sim}x$
$(1+x)^a{\sim}ax$
$a^x-1{\sim}xlna$
$e^{xlna}-1{\sim}xlna$

• $x\to🐶时，如果lim_{x\to🐶}u(x)v(x)=0，且u(x)≠0，v(x)≠0,则[1+u(x)]^{v(x)}-1{\sim}u(x)v(x)$ 先是用了ln里面趋于1，所以要u(x)趋于0，再是用的e的x次方，所以要u(x)*v(x)趋于0。
• $\text{当}f(x)\to1\text{时,}\ln f(x){\sim}f(x)-1$（ln里面趋于1，立即等价于x-1）
• $当x\to0时,\ln(x+\sqrt{x^{2}+1})\sim{x}$（反双曲正弦，奇函数，求导等于根号里面分之一）
• $\text{当}f\left(x\right)\to1\text{时,}f^{\alpha}\left(x\right)-1{\sim}\alpha\left[f\left(x\right)-1\right]$
• $1-\sqrt[n]{\cos x}\sim\frac{1}{n}*\frac{1}{2}x^2$⬆️上一个的推论⬆️
• $lim_{n{\to}∞}\sqrt[n]{a}=1(a>0)$
• $lim_{n\to∞}\sqrt{a}=1(a>0)$（数列）
• $lim_{n\to∞}\sqrt{n}=1(a>0)$（数列）

附录5【泰勒公式】

附录6【见到两眼要放光系列】

• $cos2x-1=-2sin^2x$